Neurons exploit stochastic growth to rapidly and economically build dense dendritic arbors
- PMID: 40593546
- PMCID: PMC12217211
- DOI: 10.1038/s41467-025-60800-7
Neurons exploit stochastic growth to rapidly and economically build dense dendritic arbors
Abstract
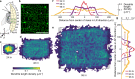
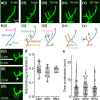
Dendrites grow by stochastic branching, elongation, and retraction. A key question is whether such a mechanism is sufficient to form highly branched dendritic morphologies. Alternatively, does dendrite geometry depend on signals from other cells or from the topological hierarchy of the growing network? To answer these questions, we developed an isotropic and homogenous mean-field model in which branch dynamics depends only on average lengths and densities: that is, without external influence. Branching was modeled as density-dependent nucleation so that no tree structures or network topology was present. Despite its simplicity, the model predicted several key morphological properties of class IV Drosophila sensory dendrites, including the exponential distribution of branch lengths, the parabolic scaling between dendrite number and length densities, the tight spacing of the dendritic meshwork (which required minimal total branch length), and the radial orientation of branches. Stochastic growth also accelerated the overall expansion rate of the arbor. We show that stochastic dynamics is an economical and rapid space-filling mechanism for building dendritic arbors without external guidance or hierarchical branching mechanisms. Our work therefore provides a general theoretical framework for understanding how macroscopic branching patterns emerge from microscopic dynamics.
© 2025. The Author(s).
Conflict of interest statement
Competing interests: The authors declare no competing interests.
Figures






Update of
-
Neurons exploit stochastic growth to rapidly and economically build dense radially oriented dendritic arbors.bioRxiv [Preprint]. 2025 Feb 24:2025.02.24.639873. doi: 10.1101/2025.02.24.639873. bioRxiv. 2025. Update in: Nat Commun. 2025 Jul 1;16(1):5903. doi: 10.1038/s41467-025-60800-7. PMID: 40060586 Free PMC article. Updated. Preprint.
Similar articles
-
Neurons exploit stochastic growth to rapidly and economically build dense radially oriented dendritic arbors.bioRxiv [Preprint]. 2025 Feb 24:2025.02.24.639873. doi: 10.1101/2025.02.24.639873. bioRxiv. 2025. Update in: Nat Commun. 2025 Jul 1;16(1):5903. doi: 10.1038/s41467-025-60800-7. PMID: 40060586 Free PMC article. Updated. Preprint.
-
Signs and symptoms to determine if a patient presenting in primary care or hospital outpatient settings has COVID-19.Cochrane Database Syst Rev. 2022 May 20;5(5):CD013665. doi: 10.1002/14651858.CD013665.pub3. Cochrane Database Syst Rev. 2022. PMID: 35593186 Free PMC article.
-
Comparison of Two Modern Survival Prediction Tools, SORG-MLA and METSSS, in Patients With Symptomatic Long-bone Metastases Who Underwent Local Treatment With Surgery Followed by Radiotherapy and With Radiotherapy Alone.Clin Orthop Relat Res. 2024 Dec 1;482(12):2193-2208. doi: 10.1097/CORR.0000000000003185. Epub 2024 Jul 23. Clin Orthop Relat Res. 2024. PMID: 39051924
-
Systemic pharmacological treatments for chronic plaque psoriasis: a network meta-analysis.Cochrane Database Syst Rev. 2021 Apr 19;4(4):CD011535. doi: 10.1002/14651858.CD011535.pub4. Cochrane Database Syst Rev. 2021. Update in: Cochrane Database Syst Rev. 2022 May 23;5:CD011535. doi: 10.1002/14651858.CD011535.pub5. PMID: 33871055 Free PMC article. Updated.
-
Maternal and neonatal outcomes of elective induction of labor.Evid Rep Technol Assess (Full Rep). 2009 Mar;(176):1-257. Evid Rep Technol Assess (Full Rep). 2009. PMID: 19408970 Free PMC article.
References
-
- Chklovskii, D. B. Synaptic connectivity and neuronal morphology: two sides of the same coin. Neuron43, 609–617 (2004). - PubMed
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

