Exploiting hidden singularity on the surface of the Poincaré sphere

Abstract

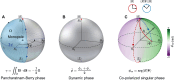
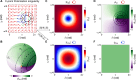
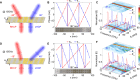
The classical Pancharatnam-Berry phase, a variant of the geometric phase, arises purely from the modulation of the polarization state of a light beam. Due to its dependence on polarization changes, it cannot be effectively utilized for wavefront shaping in systems that require maintaining a constant (co-polarized) polarization state. Here, we present a novel topologically protected phase modulation mechanism capable of achieving anti-symmetric full 2π phase shifts with near-unity efficiency for two orthogonal co-polarized channels. Compatible with -but distinct from- the dynamic phase, this approach exploits phase circulation around a hidden singularity on the surface of the Poincaré sphere. We validate this concept in the microwave regime through the implementation of multi-layer chiral metasurfaces. This new phase modulation mechanism expands the design toolbox of flat optics for light modulation beyond conventional techniques.

Fig. 1. Comparison between different phase-addressing mechanisms.

A Typical Pancharatnam-Berry phase, associated to cross-polarized phase modulation and originating from the degeneracy of the Jones matrix, corresponds to the magnetic flux of a virtual monopole of intensity −1/2 positioned at the center of the Poincaré sphere. Considering the transmission of a right incident circularly polarized wave $\mid R⟩$ through birefringent materials with eigenstate of azimuth ψ (thick blue arrow), polarization evolves along the meridian from the north to the south pole. Choosing two different meridians, two cross-polarized beams taking two different meridian trajectories would present a phase difference equal to half of the magnetic flux through the blue solid angle Ω swept counterclockwise between the two meridians (blue and dashed blacklines). B The dynamic phase is polarization-independent and only depends on mean phase ϕ = (ϕ₊ + ϕ₋)/2 of the eigenvalues exp(iϕ_±), and therefore applies to any polarization channel equally. C The evolution of polarization state and the emergence of a co-polarized phase singularity on the Poincaré sphere are governed by the system’s eigen parameters $\left(\delta ,\chi \right)$. The input state $\mid R⟩$ undergoes precession around the eigenaxis $\widehat{n}\left(\chi \right)$ by an angle $\delta$, transitioning to an intermediate state $\mid \mathrm{\Psi }⟩$, tracing the red curve. The subsequent projection back to the initial state follows the blue dashed curve, acquiring an additional phase, which is evident from the relative configuration of the initial and final $\mid R⟩$ states. The accumulated phase, solely depends on the curvature of the traversed path, has a pure geometric origin. Variation in the eigen parameters alters polarization trajectory on the Poincaré sphere and thereby modifying the accumulated geometric phase. When the eigen axis crosses the equator $\widehat{n}\left(\chi =0,\psi =constant\right)$ with $\delta =\pi$, the input $\mid R⟩$ state reverses its helicity (red dashed curve), and the accumulated geometric phase through the projective measurement depends on the shortest geodesic path. A very small variation around $\left(\delta =\pi ,\chi =0\right)$ shifts the position of $\mid \mathrm{\Psi }⟩$, affecting the projection path. This leads to a co-polarized singular phase, which lies exactly at the antipodal point |L〉 denoted with the star mark. This phase singularity emerges in complex amplitude of the co-polarized transmission channel at the Stokes parametric position of $\mid \mathrm{\Psi }⟩$, representing a topological variant of the geometric P-B phase.

Fig. 2. C-point polarization singularity and associated co-polarized singular phase in the eigen parameter space(δ, χ).

A Distribution of the polarization ellipses of $\mid \mathrm{\Psi }⟩$ in the eigen parameter space. The evolution of the input state creates a C-point polarization singularity at $\delta =\pi ,\chi =0$, containing the antipodal LHCP state at the singular point. Three different closed loops outside (solid circle), crossing (dashed circle), and encircling (dotted circle) the singular C-point are considered. B The corresponding trajectories of $\mid \mathrm{\Psi }⟩$, along with the co-polarized phase distribution are displayed on the Poincaré sphere. The yellow star represents the position on the Poincaré sphere where the singularity appears. C–F The decomposition of the $\mid \mathrm{\Psi }⟩$ into the co-and cross-polarized channels is performed by the respective projection operators, representing amplitude and phase distribution in the eigen-parameter space. Notably, at the C-point, the co-polarized phase becomes singular and circulation of this topologically protected phase enables complete 2π wavefront modulation in a spin-preserved manner.

Fig. 3. Encircling the singularity with unitary transmittance.

A Expansion of the Poincaré sphere according to the complex co-polarized transmittance. A conical surface representing the amplitude, in addition to the heat map of the projected phase at the bottom, indicates a vanishing amplitude and a rapidly changing phase from [0,2π] characteristic of phase singularity. Choosing a path that encircles the singular parameter point with unit transmittance can be realized using the designed circular birefringent meta-atoms indicated by stars. B Schematic of the structure of the circular birefringent meta-atoms and the shapes of the eight elements annotated in (A), designed to tune quasi-linearly (δ ≈ 2θ) the circular birefringence using the elements’ relative rotation angle. The C co- and D cross-polarized transmittance of an elementary meta-atom with relative rotation angle from 0° to 90°, indicating almost zero cross-polarized conversion and zero P-B phase.

Fig. 4. Results of metasurfaces for wavefronts tailoring.

A Schematic of the designed antisymmetric refractor at 10 GHz. B The designed phase profile of the co-polarized channel of RHCP (red) and LHCP (blue) at 10 GHz of refractor, which are opposite because of the conjugate coupling between the responses. The inset is the photograph of the fabricated prototype, which consists of two kinds of structures with different geometric sizes. C The measured normalized far-field patterns of the two co-polarized channels. D Schematic of the designed asymmetric refractor at 10 GHz. E The decoupled phase profile of the two co-channels, and the constituent structures in the inset show multiple geometric sizes since the dynamic phase is introduced. F The measured normalized far-field patterns of the asymmetric refractor.