Floquet-Bloch valleytronics

Abstract

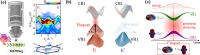
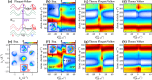
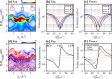
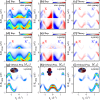
Upon time-periodic driving of electrons using electromagnetic fields, the emergence of Floquet-Bloch states enables the creation and control of exotic quantum phases. In transition metal dichalcogenides, broken inversion symmetry within each monolayer results in Berry curvature at the K and K' valley extrema, giving rise to chiroptical selection rules that are fundamental to valleytronics. Here, we bridge the gap between these two concepts and introduce Floquet-Bloch valleytronics. Using time- and polarization-resolved extreme ultraviolet momentum microscopy combined with state-of-the-art ab initio theory, we demonstrate the formation of valley-polarized Floquet-Bloch states in 2H-WSe₂ upon below-bandgap driving with circularly polarized light pulses. We investigate quantum-path interference between Floquet-Bloch and Volkov states, revealing its dependence on the valley pseudospin and light polarization. Extreme ultraviolet photoemission circular dichroism in these non-equilibrium settings reveals the potential for controlling the orbital character of Floquet-engineered states. These findings link Floquet engineering and quantum-geometric light-matter coupling in two-dimensional materials.

Fig. 1. Experimental scheme and concept of Floquet valleytronics.

a A polarization-tunable infrared pump (1.2 eV, 135 fs, 5.7 mJ/cm²) and a polarization-tunable XUV (21.6 eV) probe pulses are focused on 2H-WSe₂, in the interaction chamber of a time-of-flight momentum microscope, at an incidence angle of 65° and with the light incidence plane along the crystal mirror plane $\mathcal{M}$ (Γ-M direction). The energy-momentum cut along K-Γ-K′, recorded at pump-probe overlap and integrated over all pump IR quarter-wave plate (QWP) angles, shows the emergence of +ℏω sideband. The modulation of the IR pump polarization enables the investigation of valley-polarized Floquet states. In contrast, the modulation of the XUV polarization provides access to circular dichroism (CD-ARPES) from light-driven states. b Schematic of the Floquet-engineered electronic structure of 2H-WSe₂ around K and K′ valleys. Upon time-periodic driving using IR circularly-polarized pulse, valley-polarized Floquet states are created. For simplicity, only the topmost valence band (VB1), associated +ℏω sideband, and first conduction band (CB1) are shown. Here, Floquet-Bloch Valleytronics refers to the light-induced asymmetric population of Floquet-Bloch bands with distinct valley pseudospins, specifically K and K′, driven by different light helicities. c Schematic of the population dynamics of VB1 and CB1 induced by sub-gap coherent dressing and orbital hybridization associated with the formation of Floquet sideband.

Fig. 2. Valley- and polarization-resolved quantum path interference between Floquet-Bloch and Volkov states.

a Schematic of different coherent light-matter dressing effects, i.e., Floquet, Volkov, and quantum path interferences between Floquet and Volkov transitions. b, f Experimentally measured normalized azimuthal angular distribution of the photoemission intensity around K′ and K valleys, respectively, of the +ℏω sideband (shown in (e)) as a function of the IR QWP angle (${\theta }_{\mathrm{QWP}}^{IR}$), for p − polarized XUV probe, at the pump-probe temporal overlap. Insets represent the photoemission intensity around the K′ and K valleys of the +ℏω sideband, for quasi-circular and s − polarized pumps (cut through black dashed lines). e Constant energy contour of the first-order sideband (E - E_VBM = 0.85 eV), integrated over all ${\theta }_{\mathrm{QWP}}^{IR}$. c, d, g, h Theoretical equivalent of (b) and (f), including the contribution of both Floquet and Volkov transitions (c, g), and contribution from Volkov only (d, h).

Fig. 3. Valley-Polarized Floquet-Bloch states in 2H-WSe₂.

a Energy-momentum cut along K-Γ-K′ direction, measured at the pump-probe temporal overlap and integrated for all IR quarter-wave plate angles (${\theta }_{\mathrm{QWP}}^{IR}$). b Normalized photoemission intensity from the +ℏω sideband around Γ (black line), K (red line) and K′ (blue line) valleys, as a function of ${\theta }_{\mathrm{QWP}}^{IR}$. c Theoretical equivalent of (b), including the contribution of both Floquet and Volkov transitions. d Differential energy-momentum cut along K-Γ-K′ direction, measured at pump-probe overlap, obtained by subtracting the photoemission spectra measured using right- (RCP) and left-circularly (LCP) polarized IR driving pulses, highlights the emergence of valley-polarized +ℏω replica. e Polarization-resolved valley asymmetry of the +ℏω sideband, extracted through the normalized difference between photoemission intensity at K and K′ shown in (b). f Same as (e), but using the calculated photoemission intensities, when including the contribution of Floquet only (solid yellow line), Volkov only (dashed black line) and coherent sum of Floquet and Volkov (solid black line).

Fig. 4. XUV photoemission circular dichroism and orbital character of light-dressed states.

a Experimentally measured energy-momentum cut along K-Γ-K′ direction, at pump-probe overlap, using right-circularly-polarized IR pump and integrated for all XUV quarter-wave plate angles, and b associated CD-ARPES. c Calculated CD-ARPES for circularly-polarized IR pump, including the contribution of both Floquet and Volkov transitions using theoretical approaches described in Methods. d–f Same as (a–c), but using s − polarized IR pump. g–i Orbital-resolved contributions to the trARPES signal along K-Γ-K′ direction, using s − polarized IR pump. For each subpanel, the signal associated with the +ℏω sideband has been multiplied such that its absolute intensity matches the one from the VB.