Parametric matrix models
- PMID: 40593843
- PMCID: PMC12220823
- DOI: 10.1038/s41467-025-61362-4
Parametric matrix models
Abstract
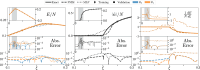
We present a general class of machine learning algorithms called parametric matrix models. In contrast with most existing machine learning models that imitate the biology of neurons, parametric matrix models use matrix equations that emulate physical systems. Similar to how physics problems are usually solved, parametric matrix models learn the governing equations that lead to the desired outputs. Parametric matrix models can be efficiently trained from empirical data, and the equations may use algebraic, differential, or integral relations. While originally designed for scientific computing, we prove that parametric matrix models are universal function approximators that can be applied to general machine learning problems. After introducing the underlying theory, we apply parametric matrix models to a series of different challenges that show their performance for a wide range of problems. For all the challenges tested here, parametric matrix models produce accurate results within an efficient and interpretable computational framework that allows for input feature extrapolation.
© 2025. The Author(s).
Conflict of interest statement
Competing interests: The authors declare no competing interests.
Figures




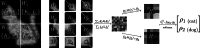

References
-
- Raissi, M., Perdikaris, P. & Karniadakis, G. E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys.378, 686–707 (2019).
-
- Karniadakis, G. E. et al. Physics-informed machine learning. Nat. Rev. Phys.3, 422–440 (2021).
-
- Schuetz, M. J., Brubaker, J. K. & Katzgraber, H. G. Combinatorial optimization with physics-inspired graph neural networks. Nat. Mach. Intell.4, 367–377 (2022).
-
- Quarteroni, A., Manzoni, A. & Negri, F. Reduced Basis Methods for Partial Differential Equations: An Introduction, vol. 92 of UNITEXT (Springer, 2015).
-
- Hesthaven, J., Rozza, G. & Stamm, B.Certified Reduced Basis Methods for Parametrized Partial Differential Equations. SpringerBriefs in Mathematics (Springer International Publishing, 2016). 10.1007/978-3-319-22470-1.
Grants and funding
LinkOut - more resources
Full Text Sources

