Anisotropic chemical bonding of lanthanide-OH molecules

Abstract

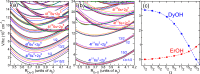
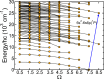
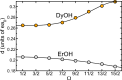
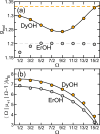
We present a theoretical study of the low lying adiabatic relativistic electronic states of lanthanide monohydroxide (Ln-OH) molecules near their linear equilibrium geometries. In particular, we focus on heavy, magnetic DyOH and ErOH relevant to fundamental symmetry tests. We use a restricted-active-space self-consistent field method combined with spin-orbit coupling as well as a relativistic coupled-cluster method to determine ground and excited electronic states. In addition, electric and magnetic dipole moments are computed with the self-consistent field method. Analysis of the results from both methods shows that the dominant molecular configuration of the ground state is one where an electron from the partially filled and anisotropic 4f orbital of the lanthanide atom moves to the hydroxyl group, leaving the closed outer-most [Formula: see text] lone electron pair of the lanthanide atom intact in sharp contrast to the bonding in alkaline-earth monohydroxides and YbOH, where an electron from the outer-most s shell moves to the hydroxyl group. For linear molecules the projection of the total electron angular momentum on the symmetry axis is a conserved quantity with quantum number Ω and we study the polynomial Ω dependence of the energies of the ground states as well as their electric and magnetic moments. We find that for both molecules Ω lies between [Formula: see text] and [Formula: see text], where the degenerate states with the lowest energy have [Formula: see text] and 1/2 for DyOH and ErOH, respectively. The zero field splittings among these Ω states is approximately [Formula: see text] [Formula: see text], where h is the Planck constant and c is the speed of light in vacuum. We find that the permanent dipole moments for both triatomics are fairly small at 0.23 atomic units and are mostly independent of Ω. The magnetic moments are closely related to that of the corresponding atomic [Formula: see text] ion in an excited electronic state. From the polynomial Ω dependences, we also realize that the total electron angular momentum is to good approximation conserved and has a quantum number of 15/2 for both triatomic molecules. We describe how this observation can be used to construct effective Hamiltonians containing spin-spin operators.

Fig. 1

Potential energies of the and electronic configurations of DyOH (panel (a)) and ErOH (panel (b)) near their equilibrium geometries as functions of the X-O separation with or Er for a linear geometry and at a fixed O-H separation of . For each configuration the curves correspond to states with different (or more precisely ). Curves with the same color have the same . The zero of energy is at the equilibrium geometry of energetically lowest potential. The potentials have been obtained with self-consistent-field calculations using basis sets that do not include excitations into 6p and 5d molecular orbitals. Panel (c) shows the splittings among the states of the configuration (colored circles). The energies have been obtained with self-consistent-field calculations using basis sets that do include excitations into 6p and 5d molecular orbitals. The dashed curves through the markers are fits to these data and are described in the text.

Fig. 2

Isosurfaces of electronic Kohn-Sham molecular orbitals (MOs) for DyOH (panels (a,b)) and ErOH (panels (c,d)) at their equilibrium, linear geometries. In all panels the small, nearly hidden cyan, red, and gray balls correspond to the locations of the lanthanide, oxygen, and hydrogen atom, respectively. Panels (a,c) show some of the MOs for the configuration where the 4f and 2p orbitals overlap. The chosen 4f orbitals for DyOH and ErOH resemble the and cubic or tesseral harmonic, respectively, while the 2p orbital resembles the cubic harmonic with the lobes aligned along the z or Ln-O axis. Similarly, panels (c,d) show some of the MOs for the configuration, where now the largest feature corresponds to the 6p orbital resembling the or cubic harmonic.

Fig. 3

Electronic eigenenergies (colored circles) of DyOH at its equilibrium, linear geometry as a function of electron projection quantum number . The zero of energy is set at that of the lowest eigenstate. The excitation energies have been obtained with self-consistent-field calculations using basis sets that do include excitations into 6p and 5d molecular orbitals. For the lowest energies, lines connecting the colored circles correspond to states of the same configuration. For the higher energies, the lines although sorted by energy, are only guides for the eye. The blue arrow highlights the transition from to between the and states. It has an electric dipole moment of .

Fig. 4

Permanent dipole moment in atomic units as function of projection quantum number of states of the electronic ground-state configuration of DyOH (orange filled circles) and ErOH (grey filled circles) at their equilibrium linear geometry. Solid black curves are polynomial fits to the data as described in the text.

Fig. 5

Molecular g factors, as defined in the text, (a) and transition magnetic moments (b) as functions of for DyOH (orange filled circles) and ErOH (grey filled circles) at their linear equilibrium geometries along the body-fixed Ln-O axis. G-factors of the pseudo-spin are defined in the text. The DyOH and ErOH molecules are in their + and + ground-state configuration, respectively. In panel (a) the dashed orange and grey lines are the experimental g factors of the level of the and configurations of and , respectively. In panel (a) the solid black curve is a polynomial in found from a fit to the data for DyOH, while the solid black curves in panel b) correspond to a fit to adjustable parameter times matrix elements of the angular momentum raising operator .