Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2025 Jul 1;15(1):20624.
doi: 10.1038/s41598-025-05852-x.

Adaptive neuro-fuzzy inference system optimization of natural rubber latex modified concrete's mechanical Properties

Efiok Etim Nyah  1   2 , David Ogbonna Onwuka  3 , Joan Ijeoma Arimanwa  3 , George Uwadiegwu Alaneme  4 , G Nakkeeran  5 , Ulari Sylvia Onwuka  6 , Chinenye Elizabeth Okere  3
Affiliations

Adaptive neuro-fuzzy inference system optimization of natural rubber latex modified concrete's mechanical Properties

Efiok Etim Nyah et al. Sci Rep. .

Abstract

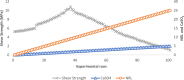
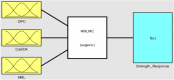
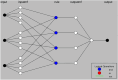
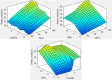
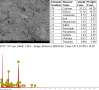
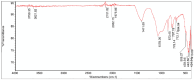
The study investigates the optimization of Natural Rubber Latex Modified Concrete (NRLMC) using an Adaptive Neuro-Fuzzy Inference System (ANFIS) to enhance predictive accuracy and material performance. Traditional laboratory testing for concrete properties is often time-consuming, costly, and prone to variability due to environmental and procedural inconsistencies. Machine learning techniques, such as ANFIS, offer a robust alternative by effectively modelling complex, nonlinear relationships in material behavior based on experimental data. In this study, laboratory experiments were conducted to examine the effects of varying Natural Rubber Latex (NRL) and calcium sulfate (CaSO4) content on NRLMC's mechanical properties. These results served as the foundation for developing an ANFIS model in MATLAB, which demonstrated high accuracy in predicting key concrete properties. The optimal mix was identified as 10% NRL and 2% CaSO4, yielding a compressive strength of 44.27 MPa and a static modulus of elasticity of 34.20 GPa. Additionally, a Poisson's ratio of 0.311, modulus of rigidity of 21.62 GPa, and shear strength of 10.78 MPa were observed at 9% NRL and 1.8% CaSO4, with strength reductions occurring beyond these thresholds. Microstructural analysis via SEM, EDS, and FTIR confirmed the effective integration of NRL into the cement matrix, enhancing density and uniformity. The ANFIS model exhibited strong predictive performance, with a root mean square error (RMSE) of 1.5434, mean absolute percentage error (MAPE) of 2.89%, and R2 of 0.9795 for the modulus of elasticity. For Poisson's ratio, RMSE was 0.7979, MAPE was 2.25%, and R2 was 0.9834. Similarly, shear modulus yielded an RMSE of 1.7208, MAPE of 2.74%, and R2 of 0.9692, while shear strength had an RMSE of 1.884, MAPE of 2.93%, and R2 of 0.9569. These results validate ANFIS as a reliable tool for accurately predicting concrete properties, reducing the need for extensive experimental trials. Furthermore, SHAP analysis highlights that OPC (%) and NRL (%) play dominant roles in influencing Ec (GPa) and shear strength (MPa), whereas CaSO4 (%) significantly impacts the Poisson's ratio and shear modulus (GPa). This study highlights the potential of NRLMC as a sustainable, high-performance material and demonstrates the efficacy of intelligent modeling for material optimization. By integrating machine learning with experimental data, this research advances the development of environmentally friendly and durable concrete, offering a scalable solution for future construction practices.

Keywords: Modulus of rigidity; Natural rubber latex; Neuro-fuzzy models; Poisson’s ratio; Static modulus of elasticity.

PubMed Disclaimer

Conflict of interest statement

Declarations. Consent to participate: All authors were highly cooperative and involved in research activities and preparation of this article. Consent for publication: All authors have declared and agreed to publish this research article. Competing interests: The authors declare no competing interests.

Figures

Fig. 1
Fig. 1
ANFIS systematic framework.
Fig. 2
Fig. 2
Test cement for experiments.
Fig. 3
Fig. 3
Test Additives (a) Natural rubber latex; (b) Calcium sulfate.
Fig. 4
Fig. 4
Mixing and casting NRLMC and test apparatus.
Fig. 5
Fig. 5
Grain size distribution of test ingredients.
Fig. 6
Fig. 6
Slump test results.
Fig. 7
Fig. 7
Compressive strength test results.
Fig. 8.
Fig. 8.
3D-surface plot showing compressive strength results of NRLMC.
Fig. 9
Fig. 9
Modulus of elasticity results of NRLMC.
Fig. 10
Fig. 10
Poisson ratio results of NRLMC.
Fig. 11
Fig. 11
3D-Surface plot showing Poisson’s ratio results of NRLMC.
Fig. 12
Fig. 12
Shear modulus results of NRLMC.
Fig. 13
Fig. 13
Shear strength results of NRLMC.
Fig. 14
Fig. 14
ANFIS model variables.
Fig. 15
Fig. 15
ANFIS model training plot: modulus of elasticity (a), Poisson ratio (b), shear modulus (c), shear strength (g).
Fig. 16
Fig. 16
ANFIS training error plot: modulus of elasticity (a), Poisson ratio (b), shear modulus (c), shear strength (d).
Fig. 17
Fig. 17
Graphical plot of trained network: modulus of elasticity (a), Poisson ratio (b), shear modulus (c), shear strength (d).
Fig. 18
Fig. 18
ANFIS training and testing datasets plot: modulus of elasticity (a), Poisson ratio (b), shear modulus (c), shear strength (d).
Fig. 19
Fig. 19
Plot of testing datasets: modulus of elasticity (a), Poisson ratio (b), shear modulus (c), shear strength (d).
Fig. 20
Fig. 20
ANFIS model structure.
Fig. 21
Fig. 21
ANFIS model variables’ membership functions (mf) plots.
Fig. 22
Fig. 22
Model Parameters’ 3D surface plots for modulus of elasticity response.
Fig. 23
Fig. 23
Model Parameters’ 3D surface plots for Poisson ratio response.
Fig. 24
Fig. 24
Model Parameters’ 3D surface plots for shear modulus response.
Fig. 25
Fig. 25
Model Parameters’ 3D surface plots for shear strength response.
Fig. 26
Fig. 26
ANFIS simulated model result versus laboratory responses.
Fig. 27
Fig. 27
SHAP analysis results.
Fig. 28
Fig. 28
SEM–EDS of control concrete sample.
Fig. 29
Fig. 29
SEM–EDS for 4%NRL of NRLMC sample.
Fig. 30
Fig. 30
SEM–EDS for 10%NRL of NRLMC sample.
Fig. 31
Fig. 31
SEM–EDS for 15%NRL of NRLMC sample.
Fig. 32
Fig. 32
FTIR spectra for control concrete sample.
Fig. 33
Fig. 33
FTIR spectra for 4% NRLMC sample.
Fig. 34
Fig. 34
FTIR spectra for 10% NRLMC sample.
Fig. 35
Fig. 35
FTIR spectra for 15% NRLMC sample.
See this image and copyright information in PMC

Similar articles

See all similar articles

References

    1. Zhou, J., Wang, G., Liu, P., Guo, X. & Xu, J. Concrete durability after load damage and salt freeze-thaw cycles. Materials (Basel).15(13), 4380. 10.3390/ma15134380 (2022). - PMC - PubMed
    1. Iro, U. I. et al. Optimization of cassava peel ash concrete using central composite design method. Sci. Rep.14, 7901. 10.1038/s41598-024-58555-0 (2024). - PMC - PubMed
    1. Alaneme George, U. & Mbadike Elvis, M. optimization of flexural strength of palm nut fibre concrete using Scheffe’s theory. Mater. Sci. Energy Technol.2(2019), 272–287. 10.1016/j.mset.2019.01.006 (2019).
    1. Topçu, İB. & Sarıdemir, M. Prediction of rubberized concrete properties using artificial neural network and fuzzy logic. Constr. Build. Mater22(4), 532–540. 10.1016/j.conbuildmat.2006.11.007 (2008).
    1. Aslani, F. & Gedeon, R. Experimental investigation into the properties of self-compacting rubberised concrete incorporating polypropylene and steel fibers. Struct. Concr.20, 267–281. 10.1002/suco.201800182 (2019).

LinkOut - more resources