Impact of layer count and thickness on spin wave modes in multilayer synthetic antiferromagnets

Abstract

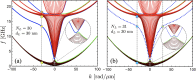
In this study, the spin-wave spectrum in multilayer synthetic antiferromagnets is calculated. The analysis focuses on the effects of varying both the thicknesses and the number of ferromagnetic layers within these structures. The results reveal that a non-reciprocal spin-wave dispersion occurs in structures with an even number of layers, while a reciprocal dispersion of two counterpropagating waves is observed for systems with an odd number of layers. As the number of layers and their thickness increase, the study identifies the distinctive presence of bulk and surface modes, with the latter being strongly affected by dynamic dipolar interactions. In multilayers with an even number of layers, such surface modes exhibit nonreciprocal behavior, maintaining their surface character only in one propagation direction. Conversely, in odd-layer systems, the symmetric counterpropagating surface modes have similar properties. Additionally, the bulk modes for both even and odd numbers of layers converge towards similar dynamic behavior as the thickness and number of layers increase. As the thickness of the ferromagnetic layers increases, the surface modes in multilayers with an odd number of layers remain localized at either the top or bottom, depending on the sign of the wave vector. In contrast, for the even case, the surface modes appear in both the top and bottom ferromagnetic layers when the layers are thin or ultrathin. However, as the ferromagnetic layer thickness increases, these modes gradually become predominantly localized at either the top or bottom of the multilayer. Finally, the study explores the application of an external magnetic field, demonstrating that surface chiral modes are absent in the saturated state, resulting in a reciprocal spin-wave dispersion. This establishes a magnetic field-mediated control over non-reciprocal localized surface modes.

Fig. 1

(a) Schematic representation of the multilayered synthetic antiferromagnet. This structure consists of $N_L$ ferromagnetic layers, each with a thickness $d_L$, separated by a spacer layer of thickness s. The ferromagnetic film is divided into sublayers of thickness $d_n$. The sublayers are exchange-coupled with $J_{\text{inter}}$ if they are at the interfaces in contact with the spacer and with $J_{\text{intra}}$ if they belong to the same ferromagnetic film. (b) Definition of the local reference system ($X_n$, $Y_n$, $Z_n$), where $Y_n=y$ is normal to the multilayer and $X_n$ lies in the film’s plane. The coordinate $Z_n$ points along the equilibrium magnetization (${\mathbf{M}}_n^{\text{eq}}$) of the n-th ferromagnetic layer.

Fig. 2

Spin wave dispersion as a function of $N_L$. The calculations are evaluated for $d_L=5$ nm and a zero external field. (a) illustrates the case of $N_L=2$, where the frequency shift is defined $\mathrm{\Delta }f=|f(-k)-f(k)|$. Highlighted modes (blue and green curves) show the two most non-reciprocal modes, namely the ones with a large $\mathrm{\Delta }f$. Bulk (BMs) and surface (SMs) modes are identified in the SW bandstructure illustrated in (e) and (f). Surface modes have chiral properties in the case of even $N_L$ [see figures (a), (c), and (e)], while for odd $N_L$, these modes behave reciprocally under the inversion of the wave vector [see figures (b), (d), and (f)]. In (c) and (f), calculated modes are compared with TetraX simulations depicted by open circles, obtaining a perfect agreement between both methods. The solid squares and circles represent highlighted modes evaluated at $k=0$, which are discussed in Fig. 3.

Fig. 3

Surface modes (squares) and the modes around them (filled circles) are shown as a function of $N_L$. The limit $k=0$ is considered in the evaluation for the cases of even (a) and odd (b) $N_L$. In (a), the insets illustrate the magnetization oscillations for the cases $N_L=2$ and $N_L=6$. In (b), the inset shows the magnetization oscillations evaluated at $N_L=5$. The time goes from zero to the period as the color goes from yellow to red, respectively.

Fig. 4

Spin-wave dispersion for $d_L=30$ nm. In (a), the case with $N_L=30$ is illustrated, while in (b), the number of layers is $N_L=31$. Bulk modes are shown on a color scale from black to red, and the surface modes are highlighted in blue and green. Note that some of the surface modes can acquire bulk properties depending on the parity of $N_L$ and the sign of the wave vector. The insets in (a) and (b) provide a magnified view of the modes within a small wave vector range, where the peculiar behavior of the surface modes can be appreciated. Circles, squares, and stars highlight the dynamic states evaluated at $|k|=30$ rad/$\mu$m, which are discussed in Fig. 5.

Fig. 5

In-plane dynamic magnetization component $m_z$ as a function of the normal coordinate y. Calculations are realized for the bulk and surface modes highlighted by markers (circles, squares, and stars) in Fig. 4. In (a), a schematic representation of the magnetization oscillations is depicted. In (b–h), the case with $N_L=30$, $d_L=30$, and $k=-30$ rad/$\mu$m is shown, where the bulk (b–d) and surface (e–h) modes are plotted as a function of the multilayer thickness. In (i–l), the system with $N_L=31$ and $d_L=30$ is considered. Panels (i) and (l) show the bulk modes, evaluated at $k=-30$ rad/$\mu$m, against the thickness of the structure. In (j) and (k), the low-frequency surface waves are depicted for $k=-30$ rad/$\mu$m and $k=+30$ rad/$\mu$m, respectively.

Fig. 6

Spin wave profiles of the surface modes for the case $N_L=30$. (a–c) corresponds to the surface mode highlighted by blue in Fig. 4, while (d–f) corresponds to the green one. The dynamic magnetization components are evaluated at $k=-30$ rad/$\mu$m, while the thickness of the ferromagnetic layers are $d_L=5$ nm, $d_L=15$ nm and $d_L=25$ nm. For better visibility, the SW profiles for ferromagnetic layers 1, 5, 10, 15, 20, 25 and 30 are illustrated. The time goes from zero ($t=0$) to the period as the color goes from yellow to red, respectively.

Fig. 7

(a) equilibrium in-plane angle $\phi$ as a function of the external field, which is applied along the z axis. The angle $\phi$ is measured from the z axis, so that $\phi =-{90}^{\circ }$ ($\phi ={90}^{\circ }$) means that the magnetization is oriented along the $-x$ (x) axis. Points P$_1^{}$ (${\mu }_0{H}_{\text{ext}}=5$ mT), P$_2^{}$ (${\mu }_0{H}_{\text{ext}}=40$ mT), P$_3^{}$ (${\mu }_0{H}_{\text{ext}}=90$ mT), and P$_4^{}$ (${\mu }_0{H}_{\text{ext}}=100$ mT) denote the equilibrium states used in the calculations of the dispersions illustrated in (b–e), respectively. The backward volume mode is highlighted in (e) with a thick dashed line.