InvSim algorithm for pre-computing airplane flight controls in limited-range autonomous missions, and demonstration via double-roll maneuver of Mirage III fighters

Abstract

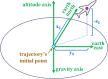
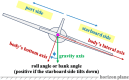
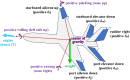
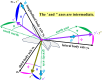
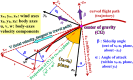
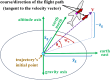
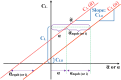
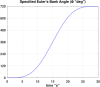
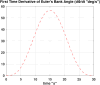
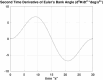
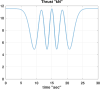
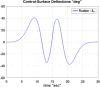
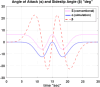
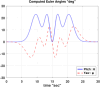
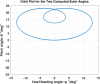
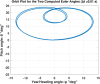
In this work, we start with a generic mathematical framework for the equations of motion (EOM) in flight mechanics with six degrees of freedom (6-DOF) for a general (not necessarily symmetric) fixed-wing aircraft. This mathematical framework incorporates (1) body axes (fixed in the airplane at its center of gravity), (2) inertial axes (fixed in the earth/ground at the take-off point), wind axes (aligned with the flight path/course), (3) spherical flight path angles (azimuth angle measured clockwise from the geographic north, and elevation angle measured above the horizon plane), and (4) spherical flight angles (angle of attack and sideslip angle). We then manipulate these equations of motion to derive a customized version suitable for inverse simulation flight mechanics, where a target flight trajectory is specified while a set of corresponding necessary flight controls to achieve that maneuver are predicted. We then present a numerical procedure for integrating the developed inverse simulation (InvSim) system in time; utilizing (1) symbolic mathematics, (2) explicit fourth-order Runge-Kutta (RK4) numerical integration technique, and (3) expressions based on the finite difference method (FDM); such that the four necessary control variables (engine thrust force, ailerons' deflection angle, elevators' deflection angle, and rudder's deflection angle) are computed as discrete values over the entire maneuver time, and these calculated control values enable the airplane to achieve the desired flight trajectory, which is specified by three inertial Cartesian coordinates of the airplane, in addition to the Euler's roll angle. We finally demonstrate the proposed numerical procedure of flight mechanics inverse simulation (InvSim) through an example case that is representative of the Mirage III family of French fighter airplanes, in which a straight subsonic flight with a double-roll maneuver over a duration of 30 s at an altitude of 5 km (3.107 mi or 16,404 ft) is inversely simulated.

Keywords: Airplane; FDM; Fixed-wing aircraft; Flight mechanics; Inverse simulation; Maneuver; Mirage III; RK4; Trajectory.

Fig. 1

Illustration of the three inertial (ground-referenced) coordinates, which are three of the four inputs to InvSim.

Fig. 2

Illustration of the roll angle, which is the fourth input to InvSim.

Fig. 3

Illustration of the four flight controls.

Fig. 4

Illustration of the three Euler angles, as well as the inertial axes and the body axes.

Fig. 5

Illustration of the wind axes and their angles (sideslip angle and angle of attack).

Fig. 6

Illustration of four tilt angles in the midplane of the airplane.

Fig. 7

Illustration of the two flight path angles.

Fig. 8

Illustration of the lift coefficient profile.

Fig. 9

Photo of Mirage III (model V 01) in flight. Permission for use was requested from the manufacturer Dassault Aviation.

Fig. 10

Profile of the roll angle in the test maneuver.

Fig. 11

Profile of the first time derivative of the roll angle in the test maneuver.

Fig. 12

Profile of the second time derivative of the roll angle in the test maneuver.

Fig. 13

Computed temporal profile of the thrust flight control during the test maneuver.

Fig. 14

Computed temporal profile of the rudder flight control during the test maneuver.

Fig. 15

Computed temporal profiles of the elevators and ailerons flight controls during the test maneuver.

Fig. 16

Computed temporal profiles of the angle of attack and sideslip angle during the test maneuver.

Fig. 17

Computed temporal profiles of the pitch and yaw angles during the test maneuver.

Fig. 18

Computed orbit plot of the pitch and yaw angles during the test maneuver at the used time step of 0.001 s.

Fig. 19

Computed orbit plot of the pitch and yaw angles during the test maneuver at a coarse time step of 0.01 s.

Fig. 20

Computed orbit plot of the pitch and yaw angles during the test maneuver at a coarser time step of 0.02 s.