Wavevector-resolved polarization entanglement from radiative cascades

Abstract

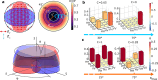
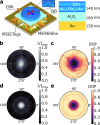
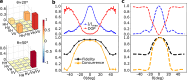
The generation of entangled photons from radiative cascades has enabled milestone experiments in quantum information science with several applications in photonic quantum technologies. Significant efforts are being devoted to pushing the performances of near-deterministic entangled-photon sources based on single quantum emitters often embedded in photonic cavities, so to boost the flux of photon pairs. The general postulate is that the emitter generates photons in a nearly maximally entangled state of polarization, ready for application purposes. Here, we demonstrate that this assumption is unjustified. We show that in radiative cascades there exists an interplay between photon polarization and emission wavevector, which can be further amplified by embedding the emitters in micro-cavities. We discuss how the polarization entanglement of photon pairs from a biexciton-exciton cascade in quantum dots strongly depends on their propagation wavevector and we even observe entanglement vanishing for large emission angles. Our experimental results, backed by theoretical modeling, yield a brand-new understanding of cascaded emission for various quantum emitters. In addition, our model provides quantitative guidelines for designing optical microcavities that retain both a high degree of entanglement and collection efficiency, moving the community one step further towards an ideal source of entangled photons for quantum technologies.

Fig. 1. Theoretical predictions for the polarization state of photons emitted by a radiative cascade.

a Bottom panel: sketch of the two emitting dipoles (blue and red arrows) with the respective isosurfaces of the radiation intensity. Top left panel: planar cut of the total emission pattern along with the direction of the electrical field oscillation for both dipole radiations, highlighting the intensity mismatch as well as the dependence of the orientation of both fields on the emission angle. Top right panel: overall degree of polarization (DOP), defined as the square root of the squared sum of the Stokes parameters (see the SI), as a function of the angles ϕ and θ. The dashed orange circle indicates a far-field region centered on the quantum emitter, corresponding to an emission angle up to θ_max. The dashed blue circles indicate different regions of θ values that select specific wavevectors. b Real part of the density matrix of the two-photon entangled state for two values of θ. The value of the concurrence for both angles is also reported. c Real part of the two-photon entangled state for two values of θ_max. The value of the concurrence for both angles is also reported.

Fig. 2. Far-field emission and degree of polarization for quantum dots in bullseye cavities.

a Sketch of the CBR sample. A detailed description of the sample features is provided in the SI. b The experimental far-field intensity distribution for a GaAs QD in a CBR cavity and c corresponding DOP distribution along the radial axis. Circles represent 10^∘ increments in the zenithal angle. The DOP is computed from the Stokes parameter sampled on the far-field radiation of the QD, which was observed through BFP imaging. d Intensity for the CBR as computed from FDTD simulations. e DOP for the CBR as computed from FDTD simulations. The full Stokes parameters distributions are reported in SI.

Fig. 3. Two-photon state and entanglement figures of merit as a function of the main collection angle for a CBR quantum dot.

a Two examples of experimental density matrices for different main collection angles θ. Due to collection from a polarized wavevector region, the two-photon state has a well-defined polarization and entanglement is lost. b Intensity and DOP profiles as a function of θ, extrapolated from the BFP measurements. They are reported with the corresponding fidelity of entanglement to the target state $∣{\varphi }^{+}⟩$ and concurrence, computed as a function of the main collection angle θ and for a small k integration range (selected by a pinhole on the BFP, see the SI). For the experimental data, we average over the azimuthal angle ϕ to obtain an average profile for radiation intensity and DOP as a function of only θ. The same quantities are reported in (c) intensity and DOP resulting from far-field FDTD simulations of the emission together with fidelity and concurrence computed on two-photon states obtained by inserting the simulated fields in Eq. (4). Error bars in the experimental data are computed assuming Poissonian distributions of coincidences and they are remarkably small due to the high number of recorded events.

Fig. 4. Two-photon state and entanglement figures of merit as a function of the collection aperture for a CBR quantum dot.

a Fidelity to the $∣{\varphi }^{+}⟩$ state and concurrence as a function of different sizes of the collection region centered around the main propagation axis. Data are shown as a function of the corresponding collection half-angle θ_max. b Experimental density matrices corresponding to different values of θ_max, showing how the two-photon polarization state follows the description of Eq. (6). Error bars in the experimental data are computed assuming Poissonian distributions of coincidences (they are remarkably small due to the high number of recorded events).