Using Deep Graph Neural Networks Improves Physics-Based Hydration Free Energy Predictions Even for Molecules Outside of the Training Set Distribution
- PMID: 40641374
- PMCID: PMC12302205
- DOI: 10.1021/acs.jpcb.5c02263
Using Deep Graph Neural Networks Improves Physics-Based Hydration Free Energy Predictions Even for Molecules Outside of the Training Set Distribution
Abstract
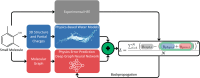
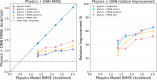
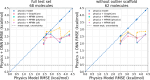
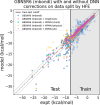
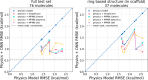
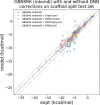
The accuracy of computational water models is crucial to atomistic simulations of biomolecules. Here we explore a decoupled framework that combines classical physics-based models with deep neural networks (DNNs) to correct residual error in hydration free energy (HFE) prediction. Our main goal is to evaluate this framework on out-of-distribution data (molecules that differ significantly from those used in training), where DNNs are known to struggle. Several common physics-based solvation models are used in the evaluation. Graph neural network architectures are tested for their ability to generalize using multiple data set splits, including out-of-distribution HFEs and unseen molecular scaffolds. Our most important finding is that for out-of-distribution data, where DNNs alone often struggle, the physics + DNN models consistently improve physics model predictions. For in-distribution data, the DNN corrections significantly improve the accuracy of physics-based models, with a final RMSE below 1 kcal/mol and a relative improvement between 40% and 65% in most cases. The accuracy of physics + DNN models tends to improve when the 6% of molecules with the highest experimental uncertainty are removed. This study provides insights into the potential and limitations of combining physics and machine learning for molecular modeling, offering a practical and generalizable strategy of using DNN as independent postprocessing correction.
Figures


Similar articles
-
Comparison of Two Modern Survival Prediction Tools, SORG-MLA and METSSS, in Patients With Symptomatic Long-bone Metastases Who Underwent Local Treatment With Surgery Followed by Radiotherapy and With Radiotherapy Alone.Clin Orthop Relat Res. 2024 Dec 1;482(12):2193-2208. doi: 10.1097/CORR.0000000000003185. Epub 2024 Jul 23. Clin Orthop Relat Res. 2024. PMID: 39051924
-
Approximating Human-Level 3D Visual Inferences With Deep Neural Networks.Open Mind (Camb). 2025 Feb 16;9:305-324. doi: 10.1162/opmi_a_00189. eCollection 2025. Open Mind (Camb). 2025. PMID: 40013087 Free PMC article.
-
Sexual Harassment and Prevention Training.2024 Mar 29. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2025 Jan–. 2024 Mar 29. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2025 Jan–. PMID: 36508513 Free Books & Documents.
-
Falls prevention interventions for community-dwelling older adults: systematic review and meta-analysis of benefits, harms, and patient values and preferences.Syst Rev. 2024 Nov 26;13(1):289. doi: 10.1186/s13643-024-02681-3. Syst Rev. 2024. PMID: 39593159 Free PMC article.
-
Signs and symptoms to determine if a patient presenting in primary care or hospital outpatient settings has COVID-19.Cochrane Database Syst Rev. 2022 May 20;5(5):CD013665. doi: 10.1002/14651858.CD013665.pub3. Cochrane Database Syst Rev. 2022. PMID: 35593186 Free PMC article.
References
Grants and funding
LinkOut - more resources
Full Text Sources

