A Hybrid Ensemble Learning Framework for Predicting Lumbar Disc Herniation Recurrence: Integrating Supervised Models, Anomaly Detection, and Threshold Optimization
- PMID: 40647627
- PMCID: PMC12249394
- DOI: 10.3390/diagnostics15131628
A Hybrid Ensemble Learning Framework for Predicting Lumbar Disc Herniation Recurrence: Integrating Supervised Models, Anomaly Detection, and Threshold Optimization
Abstract
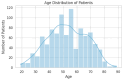
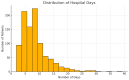
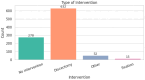
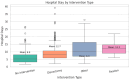
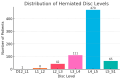
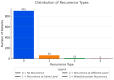
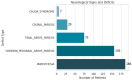
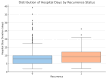
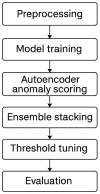
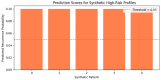
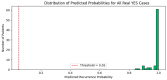
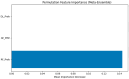
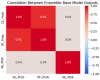
Background: Lumbar disc herniation (LDH) recurrence remains a pressing clinical challenge, with limited predictive tools available to support early identification and personalized intervention. Predicting recurrence after lumbar disc herniation (LDH) remains clinically important but algorithmically difficult due to extreme class imbalance and low signal-to-noise ratio. Objective: This study proposes a hybrid machine learning framework that integrates supervised classifiers, unsupervised anomaly detection, and decision threshold tuning to predict LDH recurrence using routine clinical data. Methods: A dataset of 977 patients from a Romanian neurosurgical center was used. We trained a deep neural network, random forest, and an autoencoder (trained only on non-recurrence cases) to model baseline and anomalous patterns. Their outputs were stacked into a meta-classifier and optimized via sensitivity-focused threshold tuning. Evaluation was performed via stratified cross-validation and external holdout testing. Results: Baseline models achieved high accuracy but failed to recall recurrence cases (0% sensitivity). The proposed ensemble reached 100% recall internally with a threshold of 0.05. Key predictors included hospital stay duration, L4-L5 herniation, obesity, and hypertension. However, external holdout performance dropped to 0% recall, revealing poor generalization. Conclusions: The ensemble approach enhances detection of rare recurrence cases under internal validation but exhibits poor external performance, emphasizing the challenge of rare-event modeling in clinical datasets. Future work should prioritize external validation, longitudinal modeling, and interpretability to ensure clinical adoption.
Keywords: autoencoder; class imbalance; clinical decision support; ensemble learning; lumbar disc herniation; machine learning; recovery/rehabilitation; recurrence prediction; threshold tuning.
Conflict of interest statement
The authors declare no conflicts of interest.
Figures
















References
-
- Fjeld O.R., Grøvle L., Helgeland J., Småstuen M.C., Solberg T.K., Zwart J.A., Grotle M. Complications, reoperations, readmissions, and length of hospital stay in 34 639 surgical cases of lumbardisc herniation. Bone Joint J. 2019;101:470–477. doi: 10.1302/0301-620X.101B4.BJJ-2018-1184.R1. - DOI - PubMed
-
- Murray C.J., Barber R.M., Foreman K.J., Ozgoren A.A., Abd-Allah S.F., Abera S.F., Aboyans V., Abraham J.P., Abubakar I., Abu-Raddad L.J., et al. Global, regional, and national disability-adjustedlife years (DALYs) for 306 diseases and injuries and healthy lifeexpectancy (HALE) for 188 countries, 1990–2013: Quantifyingthe epidemiological transition. Lancet. 2015;386:2145–2191. doi: 10.1016/S0140-6736(15)61340-X. - DOI - PMC - PubMed
-
- Kim J.-H., van Rijn R.M., van Tulder M.W., Koes B.W., de Boer M.R., Ginai A.Z., Ostelo R.W.G.J., van der Windt D.A.M.W., Verhagen A.P. Diagnostic accuracy of diagnostic imaging for lumbar disc herniation in adults with low back pain or sciatica is unknown; a systematic review. Chiropr. Man. Ther. 2018;26 doi: 10.1186/s12998-018-0207-x. - DOI - PMC - PubMed
LinkOut - more resources
Full Text Sources

