ARTEMIS integrates autoencoders and Schrödinger Bridges to predict continuous dynamics of gene expression, cell population, and perturbation from time-series single-cell data

Abstract

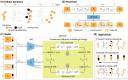
Summary: Cellular processes like development, differentiation, and disease progression are highly complex and dynamic (e.g. gene expression). These processes often undergo cell population changes driven by cell birth, proliferation, and death. Single-cell sequencing enables gene expression measurement at the cellular resolution, allowing us to decipher cellular and molecular dynamics underlying these processes. However, the high costs and destructive nature of sequencing restrict observations to snapshots of unaligned cells at discrete timepoints, limiting our understanding of these processes and complicating the reconstruction of cellular trajectories. To address this challenge, we propose ARTEMIS, a generative model integrating a variational autoencoder (VAE) with unbalanced Diffusion Schrödinger Bridge to model cellular processes by reconstructing cellular trajectories, reveal gene expression dynamics, and recover cell population changes. The VAE maps input time-series single-cell data to a continuous latent space, where trajectories are reconstructed by solving the Schrödinger bridge problem using forward-backward stochastic differential equations (SDEs). A drift function in the SDEs captures deterministic gene expression trends. An additional neural network estimates time-varying kill rates for single cells along trajectories, enabling recovery of cell population changes. Using three scRNA-seq datasets-pancreatic β-cell differentiation, zebrafish embryogenesis, and epithelial-mesenchymal transition (EMT) in cancer cells-we demonstrate that ARTEMIS: (i) outperforms state-of-art methods to predict held-out timepoints, (ii) recovers relative cell population changes over time, and (iii) identifies "drift" genes driving deterministic expression trends in cell trajectories. Furthermore, in silico perturbations show that these genes influence processes like EMT.

Availability and implementation: The code for ARTEMIS: https://github.com/daifengwanglab/ARTEMIS.

Figure 1.

Model overview. (a) Cellular processes are complex and dynamic, and undergo cell population changes driven by birth, proliferation, and death with time. (b) Single-cell sequencing provides snapshots of unaligned cells at discrete timepoints. To reconstruct cellular trajectories, we propose ARTEMIS. (c) ARTEMIS leverages single-cell time-series gene expression data. It integrates and jointly trains a VAE and unbalanced diffusion Schrödinger Bridge (uDSB) to learn a smooth latent space. The uDSB solves the SB problem using forward and backward SDEs, learning optimal backward (${\widehat{Q}}_{\widehat{\theta }}$) and forward ($Q_{\theta }$) drifts, along with VAE parameters $\phi$,$\varphi$ by optimizing $L_{\mathit{div},\widehat{\theta }}$  $L_{\mathit{div},\theta }$, and, $L_{\mathit{joint}}$, respectively. To further learn cell population changes, an additional loss $L_{\omega }$ is optimized. (d) ARTEMIS allows following downstream analysis (i) predict gene expression for unmeasured timepoints, (ii) recover relative cell population changes (infer cell status e.g. birth, proliferation, and, death) across timepoints, and (iii) learn cell drift and identify drift genes.

Figure 2.

Application to pancreatic $\beta$-cell differentiation spanning eight days (0–7). (a) 2D UMAP to show ARTEMIS’s performance on held-out timepoints (3,6). (b) Visualization of the drift inferred by ARTEMIS trained on six timepoints. (c) Top 20 drift-genes identified for $t=1$ from the forward drift $Q^{\theta }$. (d) Comparison of normalized ratios of relative cell population changes between ground truth and ARTEMIS-predicted cell statuses. (e) Ground truth versus predicted gene expression of transient TF NEUROG3.

Figure 3.

Application to zebrafish embryogenesis data across twelve stages [i.e. hours post fertilization (hpf)]. (a) 2D UMAP to show ARTEMIS’s performance on held-out timepoints (4,6,8). (b) Visualization of the drift inferred by ARTEMIS trained on nine timepoints. (c) Top 20 drift-genes identified for $t=8$. (d) Comparison of normalized ratios of relative cell population changes between ground truth and ARTEMIS-predicted cell statuses as live. (e) Boxplots showing gene expression of DE genes between cells predicted as live and dead by ARTEMIS during the interval $t=9$ to $t=10$.

Figure 4.

Application to A549 lung cancer cells undergoing TGFB1-induced EMT spanning five timepoints. (a) 2D UMAP to show ARTEMIS’s performance on held-out timepoint (4). (b) Visualization of the drift inferred by ARTEMIS trained on four timepoints. (c) Top 20 drift-genes identified for $t=2$. (d) Comparison of normalized ratios of relative cell population changes between ground truth and ARTEMIS-predicted cell statuses as live. (e) Boxplots showing gene expression of DE genes between cells predicted as live and dead by ARTEMIS during the interval $t=3$ to $t=4$.

Figure 5.

Perturbation analysis on A549 lung cancer cells undergoing TGFB1-induced EMT. ARTEMIS was initialized with 2000 cells sampled from $t=2$, either unperturbed or perturbed by TPM1 expression changes, and used to simulate trajectories to the terminal timepoint. An MLP classifier assigned cells to specific timepoints. Boxplots show the number of cells assigned to each timepoint in perturbed versus unperturbed settings. Differences were assessed using a two-sided t-test at P<0.05 (see Supplementary Note S6). (a) Underexpression ($-25$ perturbation), (b) Overexpression ($+25$ perturbation).