Expectation Value-pCCD-Based Methods for Single-Electron Properties

Abstract

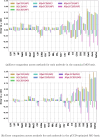
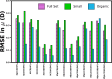
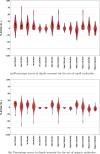
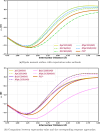
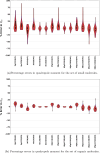
Expectation-value-coupled cluster theory (XCC) offers a simple avenue for molecular property evaluation. However, its potential has not been fully explored for the new computationally inexpensive CC models, such as pair-coupled cluster doubles (pCCD) and post-pCCD extensions. To that end, we implemented and explored one-electron reduced density matrices in the explicitly connected commutator expansion of the expectation value framework [J. Chem. Phys. 2006, 125, 184109] using pCCD, frozen pair Coupled Cluster (fpCC), and frozen pair linearized Coupled Cluster (fpLCC) variants. The expectation-value-based density matrices are calculated directly using the cluster amplitudes and are computationally cheaper than the corresponding response CC densities, as we bypass solving the computationally expensive Λ-equations. The performance of this approach, when combined with the pCCD-based methods, is assessed against the dipole and quadrupole moments of molecules of a varying chemical nature. We benchmarked our results against the response of CCSD(T) using Hartree-Fock canonical orbitals and variationally optimized pCCD orbitals. Our study highlights that localized pCCD orbitals are a good choice for computing one-electron properties of organic molecules.

1

Molecular structures of organic molecules investigated in this work. Coordinates are given in the Supporting Information. The molecular structures were drawn using the Jmol software package.

2

Signed errors with respect to CCSD­(T) (μ_Method – μ_CCSD(T)) in total dipole moments (D) for all methods using the Sadlej-pVTZ basis set for the set of small molecules investigated in this work. (HF) in (a) and (OO) in (b) denote the use of canonical and pCCD-optimized molecular orbitals, respectively.

3

Signed errors with respect to CCSD­(T) (μ_Method – μ_CCSD(T)) in total dipole moments (D) for all methods using the Sadlej-pVTZ basis set for the set of organic molecules investigated in this work. (HF) in (a) and (OO) in (b) denote the use of canonical and pCCD-optimized molecular orbitals, respectively.

4

Comparison of CC- and pCCD-based root-mean-square-error (RMSE) of dipole moments (μ in D) w.r.t. response CCSD­(T). RMSE is calculated as $\sqrt{(\sum _i^N{({\mu }_{\mathrm{M}\mathrm{e}\mathrm{t}\mathrm{h}\mathrm{o}\mathrm{d},i}-{\mu }_{\mathrm{C}\mathrm{C}\mathrm{S}\mathrm{D}(T),i})}^2)/N})$ . The sets of molecules have been described in Section . (HF) and (OO) denote the use of canonical and pCCD-optimized molecular orbitals, respectively. CO and SiSe have been excluded from the analysis.

5

Signed percentage errors w.r.t. response CCSD­(T) dipole moments (μ_Method – μ_CCSD(T))/(μ_CCSD(T)) for all methods for (a) small molecules and (b) organic molecules, using the Sadlej-pVTZ basis set. CO and SiSe have been excluded. (HF) and (OO) denote the use of canonical and pCCD-optimized molecular orbitals, respectively.

6

(a) Dipole moment surface of HF in the cc-pVDZ atomic basis set calculated with XpCCD, XCC, and XfpCC methods. (b) Dipole moment surface of HF in the cc-pVDZ atomic basis set calculated with XpCCD, XfpLCC, and their response counterparts. (OO) denotes pCCD-optimized molecular orbitals. In (b), the solid lines represent the response dipole moment surfaces, and the dashed lines show the expectation-value DMS. The FCI* curve is taken from Samanta and Köhn.

7

Signed errors with respect to CCSD­(T) in the quadrupole moment component (Q _zz ^Method – Q _zz ^CCSD(T)) for all methods using the Sadlej-pVTZ basis set for the set of small molecules investigated in this work. (HF) in (a) and (OO) in (b) denote the use of canonical and pCCD-optimized molecular orbitals, respectively.

8

Signed errors with respect to CCSD­(T) in the quadrupole moment component (Q _zz ^Method – Q _zz ^CCSD(T)) for all methods using the Sadlej-pVTZ basis set for the set of organic molecules investigated in this work. (HF) in (a) and (OO) in (b) denote the use of canonical and pCCD-optimized molecular orbitals, respectively.

9

Comparison of root-mean-square-error (RMSE) of quadrupole moment (Q _zz in a.u.) values obtained with various methods. The RMSE is calculated as $\sqrt{(\sum _i^N{(Q_{zz}^{\mathrm{M}\mathrm{e}\mathrm{t}\mathrm{h}\mathrm{o}\mathrm{d},\mathrm{i}}-Q_{zz}^{\mathrm{C}\mathrm{C}\mathrm{S}\mathrm{D}(\mathrm{T}),\mathrm{i}})}^2)/N})$ . The sets of molecules have been described in Section . (HF) and (OO) denote the use of canonical and pCCD-optimized orbitals, respectively. ClF has been excluded from the analysis.

10

Signed percentage errors with respect to CCSD­(T) reference values in the quadrupole moment component ((Q _zz ^Method – Q _zz ^CCSD(T))/Q _zz ^CCSD(T)) for all methods using the Sadlej-pVTZ basis set for the set of (a) small and (b) organic molecules investigated in this work. ClF has been excluded. (HF) and (OO) denote the use of canonical and pCCD-optimized molecular orbitals, respectively. The same range for the y-axis has been used in both plots for comparison.