A Kinetic Model of Antigen-Dependent IgG Oligomerization and Complement Binding

Abstract

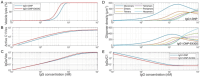
The classical complement pathway (CCP) is an essential part of the immune system, activated when complement protein C1 binds to IgG antibody oligomers on the surface of pathogens, infected or malignant cells, culminating in the formation of the membrane attack complex and subsequent cell lysis. IgG oligomers also engage immune effector cells through Fcγ receptors or complement receptors, facilitating antibody-dependent cellular cytotoxicity and phagocytosis. Understanding the factors that drive IgG oligomerization is thus crucial for improving IgG-based therapies. Herein, a kinetic model to predict oligomer formation based on IgG concentration, antigen density, IgG subclass, Fc mutants, and oligomerization inhibitors like staphylococcal protein A is developed. The underlying molecular interactions in single molecule force spectroscopy and grating coupled interferometry experiments are characterized. By fitting experimental data from high-speed atomic force microscopy experiments, key rate constants and thermodynamic parameters, including free energy changes associated with oligomerization and apply the model to predict complement-mediated lysis in liposomal vesicle-based assays, are further quantified. The presented mechanistic framework may serve as a basis for optimizing antibody engineering and pharmacokinetic/pharmacodynamic modeling in the context of immunotherapies exploiting the CCP.

Keywords: C1; IgG hexamers; IgG oligomerization; IgG subclasses; classical complement pathway; complement mediated; kinetic oligomerization model; lysis.

Figure 1

Kinetic model of antigen‐dependent IgG oligomerization. A) Upper branch of the vertical oligomerization pathway. B) Lower branch of the vertical oligomerization pathway. Fc domains, antigen‐unbound, and antigen‐bound Fab domains are colored black, white, and blue, respectively.

Figure 2

Single molecule force spectroscopy (SMFS) of IgG subclass specific Fc–Fc interactions. A) Schematic of a SMFS experiment involving a DNP‐unspecific IgG covalently linked via a PEG linker to the AFM tip and DNP‐specific IgGs bound to a DNP‐SLB generated on a glass coverslip. B) Dependence of the dissociation forces on the force loading rates (symbols; mean ± SD) and least squares fits to the Bell–Evans model (solid lines) for each IgG variant. C) Dissociation rate constant k _off (upper panel) and distance from the bound to the transition state x _β (middle panel) obtained from the fits in (B). Specificity controls employing Fc binding SpA‐B_AA and bare SLBs. D) Sketch of the Gibbs free energy landscape along the Fc–Fc reaction coordinate (separation). E) Binding probability (symbols) as a function of the encounter time for each IgG variant. The solid lines are least‐squares fits to mono‐exponential functions yielding characteristic time constants used to calculate the kinetic on‐rate constants. F) Association rate constants k _on (upper panel) obtained from (E) and equilibrium dissociation constants calculated using K _D = k _off/k _on. Fit parameters are depicted including 95% Cl. determined as described.^{[ 28} , ^{29 ]}

Figure 3

Grating coupled interferometry (GCI) characterization of IgG‐Fab‐DNP (30, 90, 270, 810 nm, 2.43, 7.29, 14.85 μm; three replicates per conc.) binding to SLBs containing A) 0.85% and B) 5% DNP. Dashed lines represent global least‐squares fits to a 1:1 Langmuir binding model.

Figure 4

IgG1‐DNP oligomer distributions obtained through 3 min incubation of 6.6–33 nm IgG1‐DNP on SLBs containing 0.85% DNP‐DPPE (lower row), 2.5% DNP‐DPPE (middle row), and 5% DNP‐DPPE (upper row). Gray bars depict experimentally determined oligomer abundances; green bars represent a global fit (together with the data presented in Figure S3–S5, Supporting Information) to our kinetic model with parameters given in Table 1. Values in the legends correspond to the total IgG densities.

Figure 5

IgG‐DNP oligomer distributions obtained through 3 min incubation of 6.6–33 nm A) IgG3‐DNP, B) IgG3‐DNP‐E430G, C) IgG4‐DNP, and D) IgG4‐DNP‐E430G on SLBs containing 5% DNP‐DPPE. Gray bars depict experimentally determined oligomer abundances; green bars represent a global fit to our kinetic model with parameters given in Table 2.

Figure 6

Transitions during IgG oligomerization involving rates A) k _1b and B–D) k ₃ (and analogously k ₄₎. The initial and final macrostates y _i each represent a certain number of energetically equivalent microstates Ω_i and associated entropy values given by S _i  = k _B ln Ω_i. The number of microstates in each initial macrostate is proportional to the volume V in which the unbound Fabs can screen for a binding partner. In the respective final macrostates on the other hand, the number of microstates is proportional to the area A on the antigenic membrane within which the Fab can access a potential antigen.

Figure 7

Simulation of liposomal vesicle‐based complement lysis assays. A) Vesicle lysis induced by varying concentrations of IgG1‐DNP and IgG1‐DNP‐E430G. B) Abundance of C1 bound to IgG1 tetramers or larger per vesicle in dependence of IgG concentration. C) Total IgGs bound per vesicle. D) IgG concentration dependence of the IgG oligomer distributions on the vesicle surface. E) C1 recruitment efficiency as a function of the IgG concentration.