Emergent microtubule properties in a model of filament turnover and nucleation

Abstract

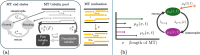
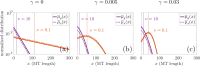
Microtubules (MTs) are dynamic protein filaments essential for intracellular organization and transport, particularly in long-lived cells such as neurons. The plus and minus ends of neuronal MTs switch between growth and shrinking phases, and the nucleation of new filaments is believed to be regulated in both healthy and injury conditions. We propose stochastic and deterministic mathematical models to investigate the impact of filament nucleation and length-regulation mechanisms on emergent properties such as MT lengths and numbers in living cells. We expand our stochastic continuous-time Markov chain model of filament dynamics to incorporate MT nucleation and capture realistic stochastic fluctuations in MT numbers and tubulin availability. We also propose a simplified partial differential equation (PDE) model, which allows for tractable analytical investigation into steady-state MT distributions under different nucleation and length-regulating mechanisms. We find that the stochastic and PDE modeling approaches show good agreement in predicted MT length distributions, and that both MT nucleation and the catastrophe rate of large-length MTs regulate MT length distributions. In both frameworks, multiple mechanistic combinations achieve the same average MT length. The models proposed can predict parameter regimes where the system is scarce in tubulin, the building block of MTs, and suggest that low filament nucleation regimes are characterized by high variation in MT lengths, while high nucleation regimes drive high variation in MT numbers. These mathematical frameworks have the potential to improve our understanding of MT regulation in both healthy and injured neurons.

Keywords: microtubule turnover; nucleation; stochastic modeling.

Figure 1:

(a) Schematic of the CTMC model of MT growth/shrinking dynamics and nucleation, where MT ends stochastically switch between growth and shrinking states and MT growth speeds depend on available free tubulin protein. New MTs appear through the nucleation mechanism, which we model by a Poisson arrival process with arrival rate $\nu$. The grey boxed portion of the schematic was previously developed in [20] and more details are given in A and B. (b) Schematic of the PDE model of MT growth dynamics at the plus end. Microtubule plus ends can switch between growth and shrinking phases, where growth depends on tubulin availability and switching from growth to shrinking depends on MT length. Nucleation of MTs occurs as a boundary condition for the growing MT population of length 0, i.e. ${\mu }_g(0,t)$.

Figure 2:

PDE model predictions of steady-state normalized length frequency log-distributions of growing (solid line) and shrinking (dashed line) MTs for $T_{\text{tot}}=1000\mu \mathrm{m}$ with (a) no length-dependent catastrophe ($\gamma =0$), (b) low level of length-dependent catastrophe ($\gamma =0.005$), and (c) high level of length-dependent catastrophe ($\gamma =0.03$). Red lines correspond to $\nu =0.1$ and purple lines correspond to $\nu =10$. Vertical colored lines indicate the steady-state average MT length, $\stackrel{-}{L}=\stackrel{-}{M}/\stackrel{-}{N}$, which we will later see is balanced by associated changes in expected MT number.

Figure 3:

Steady-state PDE model results of average number of MTs, $\stackrel{-}{N}$, versus average length of MTs, $\stackrel{-}{L}=\stackrel{-}{M}/\stackrel{-}{N}$, for $T_{\text{tot}}=700\mu \mathrm{m}$ (top row) and $T_{\text{tot}}=4000\mu \mathrm{m}$ (bottom row). Results for varying length-dependent catastrophe are shown in the first, second, and third columns, respectively. The circle, diamond, and square marker correspond to the point ($\stackrel{-}{N},\stackrel{-}{L}$) for $\gamma =0$, $\gamma =0.005$, and $\gamma =0.03$, respectively, defined in Eqs. (24) and (25). The grey region corresponds to the infeasible MT lengths and numbers for the given amount of tubulin, where the boundary of this region is found in Eq. (29). The horizontal line in each panel represents the target steady-state MT length, $L_{\mathrm{*}}$.

Figure 4:

Comparison of steady-state MT length log-distributions and empirical stochastic MT length log-distributions for (left) no length-dependent catastrophe, (middle) low length-dependent catastrophe, and (right) high length-dependent catastrophe. Top row shows log-distributions for low nucleation and bottom row illustrates the log-distributions for high nucleation levels. For all cases, $T_{\text{tot}}=1000\mu \mathrm{m}$. Solid lines show steady state densities of ${\stackrel{-}{\mu }}_g(x)+{\stackrel{-}{\mu }}_s(x)$ for various levels of nucleation corresponding to Eqs. (26) and (28), depending on the length-dependent catastrophe mechanism. Histograms are generated from 10 realizations of the MT growth dynamic stochastic model, simulated to 100 hours.

Figure 5:

Model predictions of the average number of MTs (N) versus the average length of MTs ($\stackrel{-}{L}$) from the steady-state PDE solutions (markers outlined in black, same as Fig. 3) and from 10 realizations of the stochastic model (colored point cloud) simulated up to 5 hours. Each point in the point cloud represents a pair consisting of the MT number and the average MT length ($N,L$) at each time point (second) of the stochastic simulation. Panels (a,d) show results for $\gamma =0$, panels (b,e) illustrate results for $\gamma =0.005$, and panels (c,f) represent results when $\gamma =0.03$. Results for the low tubulin level ($T_{\text{tot}}=700\mu \mathrm{m}$) are given in the top panels (a,b,c) and results for the high tubulin level ($T_{\text{tot}}=4000\mu \mathrm{m}$) are found in the bottom panels (d,e,f). The grey area represents infeasible MT lengths and MT numbers for the given tubulin amount, where the border is calculated in Eq. (29).