Sub-nanosecond all-optically reconfigurable photonics in optical fibres
- PMID: 40683883
- PMCID: PMC12276229
- DOI: 10.1038/s41467-025-61984-8
Sub-nanosecond all-optically reconfigurable photonics in optical fibres
Abstract
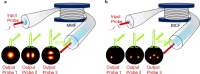
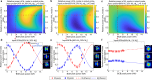
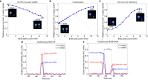
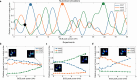
Reconfigurable photonic systems provide a versatile platform for dynamic, on-demand control and switching. Here we introduce an all-optical platform in multimode and multicore fibres. By using a low-power probe beam and a counter-propagating control beam, we achieve dynamic control over light propagation within the fibres. This setup ensures simultaneous phase-matching of all probe-control beam four-wave mixing interactions, enabling all-optical reconfiguration of the probe modal state by tuning the control beam power. Key operations such as fully tuneable power splitting and mode conversion, core-to-core switching and combination, along with remote probe characterization, are demonstrated at the sub-nanosecond time scale. Our experimental results are supported by a theoretical model that extends to fibres with an arbitrary number of modes and cores. The implementation of these operations in a single platform underlines its versatility, a critical feature of next-generation energy-efficient photonic systems. Scaling this approach to highly nonlinear materials could underpin photonic programmable hardware for optical computing and machine learning.
© 2025. The Author(s).
Conflict of interest statement
Competing interests: The authors decale no competing interests.
Figures


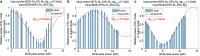
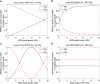
Similar articles
-
Precision medicine for mood disorders: objective assessment, risk prediction, pharmacogenomics, and repurposed drugs.Mol Psychiatry. 2021 Jul;26(7):2776-2804. doi: 10.1038/s41380-021-01061-w. Epub 2021 Apr 8. Mol Psychiatry. 2021. PMID: 33828235 Free PMC article.
-
Drugs for preventing postoperative nausea and vomiting in adults after general anaesthesia: a network meta-analysis.Cochrane Database Syst Rev. 2020 Oct 19;10(10):CD012859. doi: 10.1002/14651858.CD012859.pub2. Cochrane Database Syst Rev. 2020. PMID: 33075160 Free PMC article.
-
A Novel Design of a Portable Birdcage via Meander Line Antenna (MLA) to Lower Beta Amyloid (Aβ) in Alzheimer's Disease.IEEE J Transl Eng Health Med. 2025 Apr 10;13:158-173. doi: 10.1109/JTEHM.2025.3559693. eCollection 2025. IEEE J Transl Eng Health Med. 2025. PMID: 40657533 Free PMC article.
-
Comparison of Two Modern Survival Prediction Tools, SORG-MLA and METSSS, in Patients With Symptomatic Long-bone Metastases Who Underwent Local Treatment With Surgery Followed by Radiotherapy and With Radiotherapy Alone.Clin Orthop Relat Res. 2024 Dec 1;482(12):2193-2208. doi: 10.1097/CORR.0000000000003185. Epub 2024 Jul 23. Clin Orthop Relat Res. 2024. PMID: 39051924
-
Signs and symptoms to determine if a patient presenting in primary care or hospital outpatient settings has COVID-19.Cochrane Database Syst Rev. 2022 May 20;5(5):CD013665. doi: 10.1002/14651858.CD013665.pub3. Cochrane Database Syst Rev. 2022. PMID: 35593186 Free PMC article.
Cited by
-
Nonlinear multimode photonics on-chip.Nanophotonics. 2025 Jun 27;14(15):2507-2548. doi: 10.1515/nanoph-2025-0105. eCollection 2025 Aug. Nanophotonics. 2025. PMID: 40771421 Free PMC article. Review.
References
-
- Digonnet, M. J. Rare-earth-doped fiber lasers and amplifiers, revised and expanded. (CRC Press, Boca Raton, 2001).
-
- Stolen, R. H. & Bjorkholm, J. E. Parametric amplification and frequency conversion in optical fibers. IEEE J. Quantum Electron18, 1062–1072 (1982).
-
- Slavík, R. et al. All-optical phase and amplitude regenerator for next-generation telecommunications systems. Nat. Photon.4, 690–695 (2010).
-
- Morioka, T. & Saruwatari, M. Ultrafast all-optical switching utilizing the optical Kerr effect in polarization-maintaining single-mode fibers. IEEE J. Sel. Areas Commun.6, 1186–1198 (1988).
-
- Fatome, J., Pitois, S., Morin, P. & Millot, G. Observation of light-by-light polarization control and stabilization in optical fiber for telecommunication applications. Opt. Express18, 15311–15317 (2010). - PubMed
Grants and funding
- 202006840003/China Scholarship Council (CSC)
- EP/X040569/1/RCUK | Engineering and Physical Sciences Research Council (EPSRC)
- EP/P030181/1/RCUK | Engineering and Physical Sciences Research Council (EPSRC)
- EP/T019441/1/RCUK | Engineering and Physical Sciences Research Council (EPSRC)
- 740355/EC | EU Framework Programme for Research and Innovation H2020 | H2020 Priority Excellent Science | H2020 European Research Council (H2020 Excellent Science - European Research Council)
LinkOut - more resources
Full Text Sources

