Dissipationless transport signature of topological nodal lines

Abstract

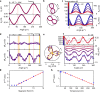
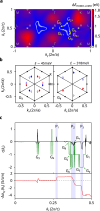
Topological materials, such as topological insulators or semimetals, usually not only reveal the non-trivial properties of their electronic wavefunctions through the appearance of stable boundary modes, but also through very specific electromagnetic responses. The anisotropic longitudinal magnetoresistance of Weyl semimetals, for instance, carries the signature of the chiral anomaly of Weyl fermions. However for topological nodal line semimetals-materials where the valence and conduction bands cross each other on one-dimensional curves in the three-dimensional Brillouin zone-such a characteristic has been lacking. Here we report the discovery of a peculiar charge transport effect generated by topological nodal lines in trigonal crystals: a dissipationless transverse signal in the presence of coplanar electric and magnetic fields, which we attribute to a Zeeman-induced conversion of topological nodal lines into Weyl nodes under infinitesimally small magnetic fields. We evidence this dissipationless topological response in trigonal PtBi₂ persisting up to room temperature, consistent with the presence of extensive topological nodal lines in the band structure of this non-magnetic material. These findings provide a pathway to engineer Weyl nodes by arbitrary small magnetic fields and reveal that bulk topological nodal lines can exhibit non-dissipative transport properties.

Fig. 1. Anomalous planar Hall effects in PtBi₂.

a Generation of an anomalous Hall conductance in nodal line semimetal systems. In a nodal line semimetal, the nodal lines do not contribute to the Chern number at zero magnetic field (left panel). Under a finite external magnetic field (right panel, red arrow), the nodal lines split into pairs of Weyl nodes of opposite chiralities (red and blue). These pairs can appear anywhere on the nodal lines (white line), including with a significant k_z separation. This leads to potential large k_z ranges of non-zero c(k_z) (pink color in the rectangle), inducing a large AHC at finite field. b Typical angular dependence of the conventional (top panel) and anomalous (bottom panel) planar Hall effects, in Cartesian (left) and polar (right) coordinates. For the conventional PHE, both the longitudinal (anisotropic magnetoresistance, R_xx, blue) and transverse (planar Hall effect, R_yx, red) resistances exhibit a π-periodic angular dependence, with a π/4-offset between them. The origin of the oscillation is set by the direction of the electric field (current). For the APHE, the angular dependence is 2π/3-periodic, with origin set by the crystal directions, and is not associated with any AMR. c Crystal structure of trigonal-PtBi₂, with layered nature and in-plane ${\mathcal{C}}_3$-symmetry highlighted. d Sample configuration. The pink arrows indicate the direction of the current. The yellow arrow corresponds to a specific crystal orientation and the black arrow indicates the direction of the magnetic field. The angle φ refers to the orientation of the in-plane magnetic field B.

Fig. 2. Standard and Anomalous Planar Hall effect in PtBi₂.

a, b Angular dependence of R_xx and R_yx at 14T, 100K in Cartesian (a) and polar coordinates (b). The fits with Equation 1 (Methods) are shown in red in a and b. The radial axis has the same range as in a. The pink bars in a and the pink dashed line in b show the current direction estimated from the fits, with a  ±5° width. c Angular dependence of R_xx and R_yx at different temperatures from 5 to 300 K, at 14T. The curves are vertically shifted for clarity. d, e Angular dependence of the residues ΔR_xx and ΔR_yx from the data in a after a background removal (see Supplementary Note B), in cartesian (d) and polar coordinates (e). A 2π/3-periodic signal is clearly visible in ΔR_yx. The pink and green bars show the previously estimated current direction and the crystal direction estimated from the fits to Supplementary Materials eq. S5, respectively, with a  ± 5° width. In e, the fit to Supplementary Materials eq. S5 is shown in green. f Bottom: angular dependence of ΔR_yx at 14T for T  =  20, 50, 100, 200, and 300 K, with fits to Supplementary Materials eq. S5 shown in green. The curves are vertically shifted for clarity. Top: Angular dependence of ΔR_yx at 14 T, 300 K, with fit in green. The 300K data was smoothed over 31° for visibility. The corresponding ΔR_xx signal is plotted in a gray line with the same scale for comparison, and shows no visible periodic signal. g Field dependence of the APHE amplitude A^APHE, showing a linear dependence above B_c  ~  2.8 T. The dashed line indicates the best linear fit for B >  2.5 T. h Temperature dependence of A^APHE, showing an exponential decay above T_c  ~  30 K, with an energy scale Δ ~6 meV. The dashed line corresponds to the best exponential fit for B ≳  30 T.

Fig. 3. Nodal lines and the origin of the anomalous Planar Hall effect in PtBi₂.

a Energy gap ΔE between HOMO and LUMO bands in the k_y, k_z (mirror) plane. The nodal loops (ΔE  =  0) appear in white. When B  ≠  0, each nodal loop splits into 6 Weyl nodes (WN, yellow points), forming 6 groups of 6-WN. The signs denote the chiralities. b Two groups of WN of HOMO-LUMO for a Zeeman energy E_Z  =  14 meV: G₃ is the 12-fold set of WNs closest to E_F already present at B  =  0, and G₈ is one of the six 6-fold groups mentioned above. The average energies of the groups are shown. Red (blue) markers denote positive (negative) chirality, while full (empty) markers denote the positive (negative) k_z position of the WN (G₃: k_z ~± 0.149, G₈: k_z ~±  0.358). Solid lines represent the mirror planes, while the dots show the high-symmetry points. c (Top) Chern number c(k_z) in an ideal (green, full HOMO) and a more realistic (black, $E_F=E_{G_3}=45.3$ meV) case, with a a Zeeman energy E_Z  =  14 meV. In the ideal case, the Chern number jumps discretely by  ±1 at each WN, while the variation is smoothed out in the realistic case. (Bottom) Anomalous Hall conductivity— Δσ_xy(k_z) calculated from the Chern signal in the realistic case (in black above). The 12 WNs from G₃ at low k_z contribute very little to the AHC, as the Berry curvature they generate is nearly compensated. Most of the AHC comes from 2 peaks in the Chern number at higher k_z, P₂, and P₃ (shown in blue). A third peak at lower k_z, P₁, attenuates the total AHC amplitude, and is found to correspond to WNs from nodal lines below the HOMO band (see Supplementary materials sec. K). Only the k_z  >  0 dependences are shown, as c(k_z) is even and Δσ_xy is odd in k_z.