EpiGeoPop: a tool for developing spatially accurate country-level epidemiological models

Abstract

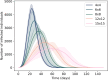
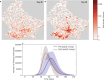
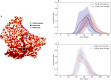
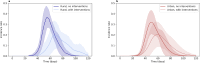
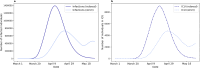
Mathematical models play a crucial role in understanding the spread of infectious disease outbreaks and influencing policy decisions. These models have aided pandemic preparedness by predicting outcomes under hypothetical scenarios and identifying weaknesses in existing frameworks; however, their accuracy, utility, and comparability are being scrutinised. Agent-based models (ABMs) have emerged as a valuable tool, capturing population heterogeneity and spatial effects, particularly when assessing potential intervention strategies. Here we present EpiGeoPop, a user-friendly tool for rapidly preparing spatially accurate population configurations of entire countries. EpiGeoPop helps to address the problem of complex and time-consuming model set-up in ABMs, specifically improving the integration of real-world spatial detail. We subsequently demonstrate the importance of accurate spatial detail in ABM simulations of disease outbreaks using Epiabm, an ABM based on Imperial College London's CovidSim with improved modularity, documentation and testing. Our simulations present a number of possible applications of ABMs where including spatially accurate data is crucial, highlighting the potential impact of EpiGeoPop in facilitating this process using multiple international data sources.

Fig. 1

EpiGeoPop workflow. EpiGeoPop uses global population density data to generate population configuration files for any country, province, or city of interest. The configuration file contains one row per ‘microcell’ (the smallest defined spatial region) with columns recording the microcell and its parent ‘cell’, the location (in x and y coordinates) of that parent cell, and the number of households, places, and susceptible individuals in that microcell. In addition, age distributions are generated on a country-level basis. The choices of region and epidemiological model, highlighted in orange, represent the elements of the workflow determined by the user. As long as the overall format of the output file from the model matches that of the input file generated by EpiGeoPop (i.e., columns representing the location’s x- and y-coordinates and the number of individuals at that location), the visualisation module can be used. This allows geographically accurate visual summaries of disease dynamics to be generated in the form of GIFs. Created with BioRender.com.

Fig. 2

Lower-density populations experience delayed and lower peaks of infections. Populations of 10,000 individuals are spread approximately uniformly over square grids of dimensions 4x4, 6x6, 8x8, 12x12, and 15x15. As such, the 4x4 model population represented the highest density, while the 15x15 is the lowest density. Lines indicate the mean over 10 simulations, while the shaded areas represent the standard deviations.

Fig. 3

Disease transmission in Luxembourg before and after changing the spatial transmission weightings. (a) Snapshot of the distribution of infections at day 40 with spatial infections guided by distance only. (b) Snapshot of the distribution of infections at day 40 with spatial infections guided by distance and population. In both snapshots darker colours indicate higher numbers of infections. (c) Total number of infections over time before (blue) and after (red) the change to the spatial transmission weightings. Results are shown as the mean ± standard deviation over 10 repetitions of each simulation. The grey dashed line indicates day 40, corresponding to the time of the above snapshots.

Fig. 4

Difference in the spread of disease in Luxembourg in rural and urban populations before and after the change to the spatial weighting. Under the new spatial weighting, the number of infections peaks earlier in the urban region than in the rural region. (a) Map highlighting the locations of the urban and rural regions selected for analysis. The urban region is highlighted in light blue and the rural region in dark blue. The location of the initial infections is indicated by the green circle. (b) Incidence rate over the course of the simulation for the selected urban (dark red) and rural (dark blue) regions before the change to the spatial weighting. (c) Incidence rate over the course of the simulation for the selected urban (light red) and rural (light blue) regions after the change to the spatial weighting. Results are shown as the mean ± standard deviation over 10 repetitions of each simulation. The incidence rate is calculated separately for each region.

Fig. 5

Incidence rate over the course of the simulation for the selected urban and rural regions (of Luxembourg City and Nommern) both with (light red and light blue, respectively) and without (dark red and dark blue, respectively) interventions. Results are shown as the mean ± standard deviation over 10 repetitions of each simulation. The incidence rate is calculated separately for each region.

Fig. 6

Trajectories of an epidemic in New Zealand with strict and relaxed interventions. The timings of these interventions followed those conducted by the New Zealand government. The effectiveness of case isolation and household quarantine was impaired in the relaxed intervention. (a) Number of infected individuals over time under both sets of interventions. (b) Number of individuals in intensive care (ICU) over time under both sets of interventions.