The Mathematics of Serocatalytic Models With Applications to Public Health Data
- PMID: 40696544
- PMCID: PMC12284347
- DOI: 10.1002/sim.70188
The Mathematics of Serocatalytic Models With Applications to Public Health Data
Abstract
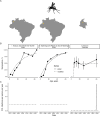
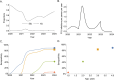
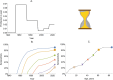
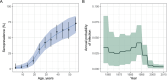
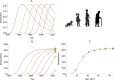
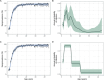
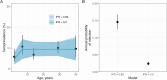
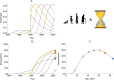
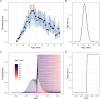
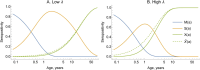
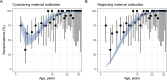
Serocatalytic models are powerful tools which can be used to infer historical infection patterns from age-structured serological surveys. These surveys are especially useful when disease surveillance is limited and have an important role to play in providing a ground truth gauge of infection burden. In this tutorial, we consider a wide range of serocatalytic models to generate epidemiological insights. With mathematical analysis, we explore the properties and intuition behind these models and include applications to real data for a range of pathogens and epidemiological scenarios. We also include practical steps and code in R and Stan for interested learners to build experience with this modeling framework. Our work highlights the usefulness of serocatalytic models and shows that accounting for the epidemiological context is crucial when using these models to understand infectious disease epidemiology.
© 2025 The Author(s). Statistics in Medicine published by John Wiley & Sons Ltd.
Conflict of interest statement
The authors declare no conflicts of interest.
Figures


Similar articles
-
Assessing the comparative effects of interventions in COPD: a tutorial on network meta-analysis for clinicians.Respir Res. 2024 Dec 21;25(1):438. doi: 10.1186/s12931-024-03056-x. Respir Res. 2024. PMID: 39709425 Free PMC article. Review.
-
Health professionals' experience of teamwork education in acute hospital settings: a systematic review of qualitative literature.JBI Database System Rev Implement Rep. 2016 Apr;14(4):96-137. doi: 10.11124/JBISRIR-2016-1843. JBI Database System Rev Implement Rep. 2016. PMID: 27532314
-
Short-Term Memory Impairment.2024 Jun 8. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2025 Jan–. 2024 Jun 8. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2025 Jan–. PMID: 31424720 Free Books & Documents.
-
The Lived Experience of Autistic Adults in Employment: A Systematic Search and Synthesis.Autism Adulthood. 2024 Dec 2;6(4):495-509. doi: 10.1089/aut.2022.0114. eCollection 2024 Dec. Autism Adulthood. 2024. PMID: 40018061 Review.
-
Sexual Harassment and Prevention Training.2024 Mar 29. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2025 Jan–. 2024 Mar 29. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2025 Jan–. PMID: 36508513 Free Books & Documents.
References
-
- Muench H., “Derivation of Rates From Summation Data by the Catalytic Curve,” Journal of the American Statistical Association 29 (1934): 25–38.
-
- Cutts F. T. and Hanson M., “Seroepidemiology: An Underused Tool for Designing and Monitoring Vaccination Programmes in Low‐and Middle‐Income Countries,” Tropical Medicine & International Health 21 (2016): 1086–1098. - PubMed
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
