A Model-Based Approach to Neuronal Electrical Activity and Spatial Organization Through the Neuronal Actin Cytoskeleton
- PMID: 40700314
- PMCID: PMC12286027
- DOI: 10.3390/mps8040076
A Model-Based Approach to Neuronal Electrical Activity and Spatial Organization Through the Neuronal Actin Cytoskeleton
Abstract
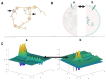
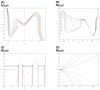
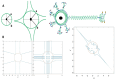
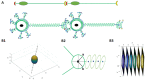
The study of neuronal electrical activity and spatial organization is essential for uncovering the mechanisms that regulate neuronal electrophysiology and function. Mathematical models have been utilized to analyze the structural properties of neuronal networks, predict connectivity patterns, and examine how morphological changes impact neural network function. In this study, we aimed to explore the role of the actin cytoskeleton in neuronal signaling via primary cilia and to elucidate the role of the actin network in conjunction with neuronal electrical activity in shaping spatial neuronal formation and organization, as demonstrated by relevant mathematical models. Our proposed model is based on the polygamma function, a mathematical application of ramification, and a geometrical definition of the actin cytoskeleton via complex numbers, ring polynomials, homogeneous polynomials, characteristic polynomials, gradients, the Dirac delta function, the vector Laplacian, the Goldman equation, and the Lie bracket of vector fields. We were able to reflect the effects of neuronal electrical activity, as modeled by the Van der Pol equation in combination with the actin cytoskeleton, on neuronal morphology in a 2D model. In the next step, we converted the 2D model into a 3D model of neuronal electrical activity, known as a core-shell model, in which our generated membrane potential is compatible with the neuronal membrane potential (in millivolts, mV). The generated neurons can grow and develop like an organoid brain based on the developed mathematical equations. Furthermore, we mathematically introduced the signal transduction of primary cilia in neurons. Additionally, we proposed a geometrical model of the neuronal branching pattern, which we described as ramification, that could serve as an alternative mathematical explanation for the branching pattern emanating from the neuronal soma. In conclusion, we highlighted the relationship between the actin cytoskeleton and the signaling processes of primary cilia. We also developed a 3D model that integrates the geometric organization unique to neurons, which contains soma and branches, such that the mathematical model represents the interaction between the actin cytoskeleton and neuronal electrical activity in generating action potentials. Next, we could generalize the model into a cluster of neurons, similar to an organoid brain model. This mathematical framework offers promising applications in artificial intelligence and advancements in neural networks.
Keywords: actin cytoskeleton; action potential; mathematical modeling; neuronal signaling; organoid brain; primary cilia.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
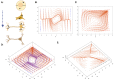
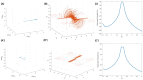
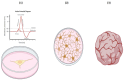
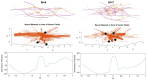
Similar articles
-
Short-Term Memory Impairment.2024 Jun 8. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2025 Jan–. 2024 Jun 8. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2025 Jan–. PMID: 31424720 Free Books & Documents.
-
Immunogenicity and seroefficacy of pneumococcal conjugate vaccines: a systematic review and network meta-analysis.Health Technol Assess. 2024 Jul;28(34):1-109. doi: 10.3310/YWHA3079. Health Technol Assess. 2024. PMID: 39046101 Free PMC article.
-
Signs and symptoms to determine if a patient presenting in primary care or hospital outpatient settings has COVID-19.Cochrane Database Syst Rev. 2022 May 20;5(5):CD013665. doi: 10.1002/14651858.CD013665.pub3. Cochrane Database Syst Rev. 2022. PMID: 35593186 Free PMC article.
-
The Lived Experience of Autistic Adults in Employment: A Systematic Search and Synthesis.Autism Adulthood. 2024 Dec 2;6(4):495-509. doi: 10.1089/aut.2022.0114. eCollection 2024 Dec. Autism Adulthood. 2024. PMID: 40018061 Review.
-
Comparison of self-administered survey questionnaire responses collected using mobile apps versus other methods.Cochrane Database Syst Rev. 2015 Jul 27;2015(7):MR000042. doi: 10.1002/14651858.MR000042.pub2. Cochrane Database Syst Rev. 2015. PMID: 26212714 Free PMC article.
References
-
- Shim S., Goyal R., Panoutsopoulos A.A., Balashova O.A., Lee D., Borodinsky L.N. Calcium dynamics at the neural cell primary cilium regulate Hedgehog signaling–dependent neurogenesis in the embryonic neural tube. Proc. Natl. Acad. Sci. USA. 2023;120:e2220037120. doi: 10.1073/pnas.2220037120. - DOI - PMC - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources

