Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2025 Jul 17;9(3):842-868.
doi: 10.1162/netn_a_00453. eCollection 2025.

Joint estimation of source dynamics and interactions from MEG data

Narayan Puthanmadam Subramaniyam  1 , Filip Tronarp  2 , Simo Särkkä  2 , Lauri Parkkonen  1
Affiliations

Joint estimation of source dynamics and interactions from MEG data

Narayan Puthanmadam Subramaniyam et al. Netw Neurosci. .

Abstract

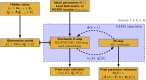
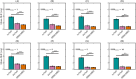
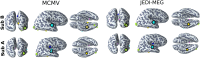
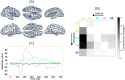
Current techniques to estimate directed functional connectivity from magnetoencephalography (MEG) signals involve two sequential steps: (a) estimation of the sources and their amplitude time series from the MEG data and (b) estimation of directed interactions between the source time series. However, such a sequential approach is not optimal as it leads to spurious connectivity due to spatial leakage. Here, we present an algorithm to jointly estimate the source and connectivity parameters using Bayesian filtering. We refer to this new algorithm as JEDI-MEG (Joint Estimation of source Dynamics and Interactions from MEG data). By formulating a state-space model for the locations and amplitudes of a given number of sources, we show that estimation of their connections can be reduced to a system identification problem. Using simulated MEG data, we show that the joint approach provides a more accurate reconstruction of connectivity parameters than the conventional two-step approach. Using real MEG responses to visually presented faces in 16 subjects, we also demonstrate that our method gives source and connectivity estimates that are both physiologically plausible and largely consistent across subjects. In conclusion, the proposed joint estimation approach outperforms the traditional two-step approach in determining functional connectivity in MEG data.

Keywords: Bayesian filtering; Functional connectivity; MEG; Source localization.

Plain language summary

Functional connectivity is currently estimated from electromagnetic brain signals such as magnetoencephalography (MEG) in two consecutive steps: First, the inverse problem is solved to estimate the locations and temporal dynamics of brain sources. Second, connectivity metrics are computed between these estimated sources. This approach suffers from the limitation that the information provided by the connectivity structure is not exploited in the estimation of source activity and vice versa. Here, we present a novel algorithm, utilizing Bayesian filtering, to jointly estimate the source and connectivity parameters to overcome this limitation. Compared with state-of-the-art two-step approaches, our method provides a more accurate reconstruction of the connectivity parameters, which we demonstrate using a standard connectivity benchmark simulation and an electrocorticography-based simulation of MEG data. We also applied our method to real MEG responses (open-access dataset) to visually presented faces in 16 subjects, and the results show that our approach provides source and connectivity estimates that are both physiologically plausible and largely consistent across subjects. Overall, this work contributes to methodological advances in estimating functional connectivity from MEG data.

PubMed Disclaimer

Conflict of interest statement

Competing Interests: The authors have declared that no competing interests exist.

Figures

<b>Figure 1.</b>
Figure 1.
Schematic illustration of the JEDI-MEG method.
<b>Figure 2.</b>
Figure 2.
MVAR simulations. (A) Unidirectional interaction between the two sources q1 and q2 with q3 as a noninteracting source (Type-I). (B) Unidirectional interactions between the three sources (Type-II).
<b>Figure 3.</b>
Figure 3.
MVAR simulations. The number (percentage) of correctly identified sources (NOC) at SNRbrain = 1, 3, 5, and 10 for Type-I (A–D) and Type-II (E–H) scenarios. The measurement noise SNR was fixed to 5, and the error bars represent the standard deviation. *p < 0.05, **p < 0.01, and ***p < 0.001.
<b>Figure 4.</b>
Figure 4.
MVAR simulations. SLE at SNRbrain = 1, 3, 5, and 10 for Type-I (A–D) and Type-II (E–H) scenarios. The measurement noise SNR was fixed to 5, and the error bars represent the standard deviation. *p < 0.05, **p < 0.01, and ***p < 0.001.
<b>Figure 5.</b>
Figure 5.
MVAR simulations. REs of connectivity coefficients at SNRbrain = 1, 3, 5, and 10 for Type-I (A–D) and Type-II (E–H) scenarios. The measurement noise SNR was fixed to 5, and the error bars represent the standard deviation. *p < 0.05, **p < 0.01, and ***p < 0.001.
<b>Figure 6.</b>
Figure 6.
MVAR simulations. FPRs of identified functional connections at SNRbrain = 1, 3, 5, and 10 for Type-I (A–D) and Type-II (E–H) scenarios. The measurement noise SNR was fixed to 5, and the error bars represent the standard deviation. *p < 0.05, **p < 0.01, and ***p < 0.001.
<b>Figure 7.</b>
Figure 7.
MVAR simulations. TPRs of identified functional connections at SNRbrain = 1, 3, 5, and 10 (A–D) for interacting sources. The measurement noise SNR was fixed to 5, and the error bars represent the standard deviation. *p < 0.05, **p < 0.01, and ***p < 0.001.
<b>Figure 8.</b>
Figure 8.
ECoG-based MEG simulations. Source estimates obtained by the MCMV and JEDI-MEG approaches for two example subjects. The estimated (no outline) and true (black outline) sources are shown in green (Source 1), yellow (Source 2), and cyan (Source 3). The estimated extra sources are in blue and magenta.
<b>Figure 9.</b>
Figure 9.
ECoG-based MEG simulations in one subject analyzed with JEDI-MEG. Ground truth and estimates of (A) source locations and (B) source amplitudes. Source 1 (S1, green), Source 2 (S2, yellow), and Source 3 (S3, cyan) with the true locations encircled in black and the true time courses shown as dashed black lines. The extra (inactive) sources are shown in magenta and blue (S4 and S5). (C) The ground-truth and (D) estimated connectivity from MVAR coefficients. The columns and rows represent outward and inward connections.
<b>Figure 10.</b>
Figure 10.
ECoG-based MEG simulations in one subject analyzed with the two-step approach (MCMV beamformer and MVAR fitting). Ground truth and estimates of (A) source locations and (B) source amplitudes. Source 1 (S1, green), Source 2 (S2, yellow), and Source 3 (S3, cyan) with the true locations encircled in black and the true time courses shown as dashed black lines. The extra (inactive) sources are shown in magenta and blue (S4 and S5). (C) The ground-truth and (D) estimated connectivity from MVAR coefficients. The columns and rows represent outward and inward connections.
<b>Figure 11.</b>
Figure 11.
ECoG-based MEG simulations. Maximum SLE across the three sources for the LCMV, MCMV, and JEDI-MEG methods.
<b>Figure 12.</b>
Figure 12.
ECoG-based MEG simulations. TPR and FPR for the JEDI-MEG method and the two-step approach using MCMV.
<b>Figure 13.</b>
Figure 13.
Real MEG data. JEDI-MEG-estimated source locations (A), directed functional connections (B), and amplitudes (C) in one subject. The connectivity matrix represents the maximum absolute coefficients of the MVAR matrix across all model orders (P = 15) and is normalized to the maximum value. In the connectivity matrix, the columns and rows represent outward and inward connections.
<b>Figure 14.</b>
Figure 14.
Real MEG data. Group-level (N = 16) estimates of source locations (A), directed functional connections (B), and amplitudes (C) by JEDI-MEG. The indicated locations are the source-cluster centroids, the time courses are the averages of those of individual sources in each cluster, and the connectivity plots are derived from the connectivity matrices averaged across subjects. In the connectivity matrix, the columns and rows represent outward and inward connections.
See this image and copyright information in PMC

Similar articles

See all similar articles

References

    1. Baccalá, L. A., Sameshima, K., & Takahashi, D. Y. (2007). Generalized partial directed coherence. In 2007 15th International Conference on Digital Signal Processing (pp. 163–166). 10.1109/ICDSP.2007.4288544 - DOI
    1. Bastos, A. M., & Schoffelen, J.-M. (2016). A tutorial review of functional connectivity analysis methods and their interpretational pitfalls. Frontiers in Systems Neuroscience, 9, 175. 10.3389/fnsys.2015.00175, - DOI - PMC - PubMed
    1. Casella, G., & Robert, C. P. (1996). Rao-Blackwellisation of sampling schemes. Biometrika, 83(1), 81–94. 10.1093/biomet/83.1.81 - DOI
    1. Cheung, B. L. P., Riedner, B. A., Tononi, G., & Van Veen, B. D. (2010). Estimation of cortical connectivity from EEG using state-space models. IEEE Transactions on Biomedical Engineering, 57(9), 2122–2134. 10.1109/TBME.2010.2050319, - DOI - PMC - PubMed
    1. Davies-Thompson, J., & Andrews, T. J. (2012). Intra- and interhemispheric connectivity between face-selective regions in the human brain. Journal of Neurophysiology, 108(11), 3087–3095. 10.1152/jn.01171.2011, - DOI - PMC - PubMed

LinkOut - more resources