A Simple Approximate Bayesian Inference Neural Surrogate for Stochastic Petri Net Models

Abstract

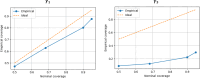
Stochastic Petri Nets (SPNs) are an increasingly popular tool of choice for modeling discrete-event dynamics in areas such as epidemiology and systems biology, yet their parameter estimation remains challenging in general and in particular when transition rates depend on external covariates and explicit likelihoods are unavailable. We introduce a neural-surrogate (neural-network-based approximation of the posterior distribution) framework that predicts the coefficients of known covariate-dependent rate functions directly from noisy, partially observed token trajectories. Our model employs a lightweight 1D Convolutional Residual Network trained end-to-end on Gillespie-simulated SPN realizations, learning to invert system dynamics under realistic conditions of event dropout. During inference, Monte Carlo dropout provides calibrated uncertainty bounds together with point estimates. On synthetic SPNs with 20% missing events, our surrogate recovers rate-function coefficients with an RMSE = 0.108 and substantially runs faster than traditional Bayesian approaches. These results demonstrate that data-driven, likelihood-free surrogates can enable accurate, robust, and real-time parameter recovery in complex, partially observed discrete-event systems.

Fig. A.1.

(a) Predicted means versus true values for within- and between-patch transition rates’ single-term coefficients, with uncertainty bars. (b) Empirical $\pm 1\sigma$ coverage of those predictions.

Fig. A.2.

(a) Predicted means versus true values for within- and between-patch transition rates’ interaction-term coefficients, with uncertainty bars. (b) Empirical $\pm 1\sigma$ coverage of those predictions.

Fig. A.3.

Predicted means versus true values for the mortality rate single-term coefficient ${\rho }_1$ as well as its empirical $\pm 1\sigma$ coverage

Fig. A.4.

Distribution of Predicted means and true values for all Parameters

Fig. 1.

A visual representation of a simple Petri Net. $P_i^{\prime }s$ represent the places (circles) which contains the markings (dark dots). $t_i^{\prime }s$ denotes the transitions (rectangles). The arrows are directed arcs between a place and a transition, which can be assigned specific weights

Fig. 2.

Model Pipeline

Fig. 3.

(a) Represents within and between patch infection, recovery and mortality dynamics (b) Represents between patch migration dynamics (Note: (a) and (b) together form one model). Double arcs indicate tokens to and from a place and transition

Fig. 4.

Uncertainty calibration curves for selected parameters

Fig. 5.

True and predicted sample parameters. The blue points represent the predicted sample parameters with $\pm 1\sigma$ error bars

Fig. 6.

True parameter mean compared to overall predicted parameter mean with $\pm 1\sigma$