NANUQ+: A divide-and-conquer approach to network estimation
- PMID: 40713832
- PMCID: PMC12297685
- DOI: 10.1186/s13015-025-00274-w
NANUQ+: A divide-and-conquer approach to network estimation
Abstract
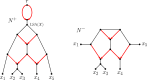
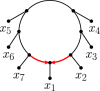
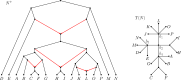
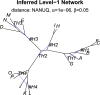
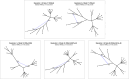
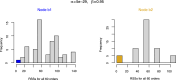
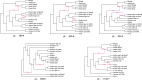
Inference of a species network from genomic data remains a difficult problem, with recent progress mostly limited to the level-1 case. However, inference of the Tree of Blobs of a network, showing only the network's cut edges, can be performed for any network by TINNiK, suggesting a divide-and-conquer approach to network inference where the tree's multifurcations are individually resolved to give more detailed structure. Here we develop a method, , to quickly perform such a level-1 resolution. Viewed as part of the NANUQ pipeline for fast level-1 inference, this gives tools for both understanding when the level-1 assumption is likely to be met and for exploring all highly-supported resolutions to cycles.
Keywords: Level-1; Multispecies coalescent; Phylogenetic network; Tree of blobs.
© 2025. The Author(s).
Conflict of interest statement
Declarations. Ethics approval and consent to participate: Not applicable. Consent for publication: Not applicable. Competing interests: Not applicable.
Figures








References
-
- Kong S, Swofford DL, Kubatko LS. Inference of phylogenetic networks from sequence data using composite likelihood. Syst Biol. 2024. 10.1093/sysbio/syae054. - PubMed
-
- Wen D, Nakhleh L. Coestimating reticulate phylogenies and gene trees from multilocus sequence data. Syst Biol. 2017;67(3):439–57. 10.1093/sysbio/syx085. - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

