A dephasing sweet spot with enhanced dipolar coupling

Abstract

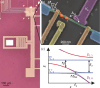
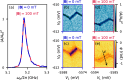
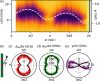
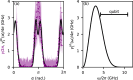
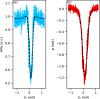
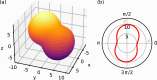
Two-level systems (TLSs) are the basic units of quantum computers but face a trade-off between operation speed and coherence due to shared coupling paths. Here, we investigate a TLS given by a singlet-triplet (ST+) transition. We identify a magnetic-field configuration that maximizes dipole coupling while minimizing total dephasing, forming a compromise-free sweet spot that mitigates this fundamental trade-off. The TLS is implemented in a crystal-phase-defined double-quantum dot in an InAs nanowire. Using a superconducting resonator, we measure the spin-orbit interaction (SOI) gap, the spin-photon coupling strength, and the total TLS dephasing rate as a function of the in-plane magnetic-field orientation. Our theoretical description postulates phonons as the dominant noise source. The compromise-free sweet spot originates from the SOI, suggesting that it is not restricted to this material platform but might find applications in any material with SOI. These findings pave the way for enhanced nanomaterial engineering for next-generation qubit technologies.

Keywords: Electronic devices; Electronic properties and materials; Nanowires; Qubits; Superconducting devices.

Fig. 1. Superconducting resonator coupled to singlet-triplet two-level system (TLS) in a crystal-phase nanowire (NW).

a Optical microscope image of the device showing a half-wave NbTiN resonator with a characteristic impedance of 2.1 kΩ. In the middle of the center conductor, a dc bias line is connected via a meandered inductor. b False-colored scanning electron micrograph of the crystal-phase NW device (image is rotated by  − 90° with respect to a). The NW is placed at the position indicated in (a), and the purple gate line is galvanically connected to the resonator at its voltage anti-node. Tunnel barriers are highlighted in red. Using the gate voltages V_L and V_R, the device is operated with an even electron filling as depicted schematically. The spin-orbit gap Δ_SO corresponds to the indicated spin-rotating tunnel transition, which forms the TLS. The in-plane magnetic field angle α is varied during the experiments using a vector magnet that controls the magnetic field B. c Level diagram for an even electron occupation as a function of the electrostatic detuning ε in the presence of strong SOI and finite magnetic field exhibiting singlet (S) and triplet (T) states. Subscripts denote the filling of the left and right dots, and the superscript denotes the spin quantum number of the triplet states (see methods). The avoided crossing between the spin-polarized triplet state T⁺ and the low-energy singlet state at ε = ε₀ is detected using the resonator.

Fig. 2. Characterization of the hybrid device.

a Resonator transmission ${\left(A/A_0\right)}^2$ as function of probe frequency ω_p. Fits to a Lorentzian result in the resonance frequency ω₀/2π = 5.1854 ± 0.0002 GHz, and decay rate κ/2π = 21.2 ± 0.4 MHz independent of the magnetic-field amplitude ∣B∣. The magnetic-field resilience of the resonator enables resonator-based investigation of the double-quantum dot (DQD). b–e Transmission ${\left(A/A_0\right)}^2$ and phase φ close to resonance frequency as a function of gate voltages V_L and V_R applied to the DQD as illustrated in Fig. 1(b) at zero field and at ∣B∣ = 100 mT. Position and shape of the observed inter-dot transition signal vary as a function of ∣B∣ due to an interaction of the resonator with spinful DQD levels. In the remainder of the manuscript, the DQD detuning ε is varied by applying V_L and V_R along the arrow indicated in (e).

Fig. 3. Two-level system (TLS) parameters as a function of in-plane field angle at ∣B∣ = 100 mT.

a Phase of the resonator transmission φ as function of electrostatic detuning ε and in-plane magnetic field angle α. The detuning ε, was calculated from the applied voltages, using the gate-to-dot lever arms (see Table 1). The dashed curve corresponds to the position of the inter-dot transition in the theoretical model, ε = ε₀, to which a linear trend was added accounting for a drift of the gate voltage. b Schematic showing the alignment of the magnetic field B with respect to the nanowire (NW), where the NW color scheme represents the crystal-phase structure according to Fig. 1b. c Spin-orbit gap Δ_so as function of α. d Coupling strength g_eff between the TLS and the resonator as function of α. e TLS dephasing rate γ as function of α. When the field is parallel to the NW, α = ± π/2, a compromise-free sweet spot is found where maximal TLS transition frequency and coupling strength coincide with minimal total dephasing rate. c–e are extracted using input-output theory. The streaks symbolize the uncertainty of the fit. This uncertainty is a consequence of the uncertainty of the gate lever arms, which forms the most significant source of uncertainty in our experiment and is stated in the caption of Table 1. All curves overlaid on the data result from the theoretical model described in the main text, using a single set of fit parameters. During the measurement, a charge relocation occurred at a magnetic-field angle α ~1.9π resulting in missing data for α ∈ [0, 0.1π] ∪ [0.19π, 2π) in all subfigures.

Fig. 4. Phonons as possible decoherence source.

a Measured dephasing rate γ as a function of in-plane angle α (purple). The experimental data is plotted as purple points, and the error bar is given by a purple stripe. The error bars are dominated by the error associated with the gate-lever arm uncertainty. The black curve is the numerically calculated relaxation rate ${\gamma }_1^{\mathrm{ph}}\left(\alpha \right)$ originating from deformational phonons (see Section Decoherence). b Analytical relaxation rate ${\gamma }_1^{\mathrm{ph}}\left(\omega \right)$ as function of phonon frequency ω (see Equation (27) in Supplementary for details). The TLS operates in the frequency range as indicated with a negative slope of ${\gamma }_1^{\mathrm{ph}}\left(\omega \right)$. This explains the anti-correlation between the SOI gap Δ_so and the dephasing rate γ - a possible reason for the compromise-free sweet spot formation.

Fig. 5. Linetrace with input-output theory fit at α = π/2.

a Measured amplitude, A/A₀, as a function of the virtual gate voltage, V_ε which is a linear superposition of the gate voltages V_R and V_L along the detuning direction (arrow in Fig. 2e). Its amplitude is defined such that $\mid V_{\epsilon }\mid =\sqrt{V_R^2+V_L^2}$. b Measured phase φ as a function of detuning gate voltage V_ε. The data is a linecut of Fig. 3a at α = π/2. The dashed curves are fits to Eq. (6).

Fig. 6. Visualization of the anisotropic g-tensor.

a Normalized Zeeman field strength $\mid \mathbf{B}\underset{\_}{g}\mid /\mid \mathbf{B}\mid$, where the g-tensor $\underset{\_}{g}$ is defined according to Eq. (10). A characteristic peanut shape is exhibited. b Cross-section of a in the x-y plane at z = 0 as a function of the in-plane angle α. The nanowire is aligned parallel to the y axis.