Simon's Algorithm in the NISQ Cloud

Abstract

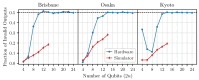
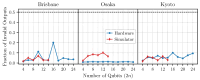
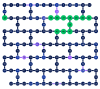
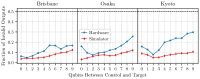
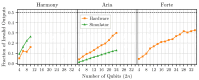
Simon's algorithm was one of the first to demonstrate a genuine quantum advantage in solving a problem. The algorithm, however, assumes access to fault-tolerant qubits. In our work, we use Simon's algorithm to benchmark the error rates of devices currently available in the "quantum cloud". As a main result, we objectively compare the different physical platforms made available by IBM and IonQ. Our study highlights the importance of understanding the device architectures and topologies when transpiling quantum algorithms onto hardware. For instance, we demonstrate that two-qubit operations on spatially separated qubits on superconducting chips should be avoided.

Keywords: NISQ computing; Simon’s algorithm; quantum advantage.

Figure A1

The performance of Simon’s algorithm using the complex oracle, cf. Figure 4a, at various sizes on IBM Osaka and simulator after the major update to Qiskit.

Figure 1

Quantum circuit diagram for Simon’s algorithm: Note the use of two quantum registers of size n, both initialized to the zero state $|0\rangle$, as well as the oracle $U_f$. The algorithm uses two Hadamard transformations and $U_f$ to create a superposition over all the size n bitstrings that are orthogonal to the secret string s. An iteration of the algorithm is successful if the final measurement result is indeed orthogonal to s (this is always true in the noise-free case). The entire algorithm is successful if a complete set of $n-1$ linearly independent bitstrings is measured, and the resulting system is solved classically in polynomial time.

Figure 2

Device topologies for IBM computers [51]: The color of qubits and connections represents the single qubit readout error and ECR error, respectively, at the time the image was taken. Lighter colors correspond to higher error rates. For single qubit readout errors, the scale ranges from $3.6\times {10}^{-3}$ to $3.45\times {10}^{-1}$, with a median of $1.45\times {10}^{-2}$. For two qubit ECR errors, the scale ranges from $2.31\times {10}^{-3}$ to $1.057\times {10}^{-1}$, with a median of $8.002\times {10}^{-2}$.

Figure 3

Device topologies for IonQ computers [53]: Observe that IonQ’s trapped-ion computers have full all-to-all connectivity.

Figure 4

Complex and simple oracle for Simon’s algorithm. Each dotted wire represents $(n-2)$ qubits, and all operations on dotted wires are repeated following the pattern across all qubits.

Figure 5

Simon’s algorithm was performed for the complex oracle at various sizes on IBM devices and simulators, cf. Figure 4a. By ∼12 qubits, the real device hovers around $50\%$ algorithmic error, which is indistinguishable from randomly guessing solutions to the problem from the space of all possibilities. See Appendix B for results obtained after a major Qiskit update released in May 2024.

Figure 6

Simon’s algorithm performed for the simple oracle at various sizes on IBM devices and simulators, cf. Figure 4b.

Figure 7

The layout of a transpiled circuit implementing Simon’s algorithm with the complex oracle for $n=5$ on IBM Osaka. Active qubits are marked in green, and unused qubits are depicted in blue or purple. As in Figure 2, the color of the unused qubits indicates the magnitude of readout error present during the device calibration, with lighter values indicating more error. It is worth noting that all used qubits marked in green originally appeared in dark blue, indicating comparatively little readout error. Note that after transpiliation, qubit 18, although active, is idle for the duration of the algorithm and does not interact with the other active qubits. All other active qubits interact directly with one or two other qubits via entangling operations.

Figure 8

Failure of CNOT gates as a function of spatial separation. Before compilation, the control bit was selected to be qubit 39 for each experiment, and the target bit ranged from bit 40 to 49 (cf. Figure 2 and Figure 7).

Figure 9

Simon’s algorithm performed at various sizes on IonQ devices and simulators. Note that the Forte device does not yet have a corresponding simulator.