Numerical Simulation of Hybrid Electric-Structural Control for Microdroplet Formation in Ribbed T-Junction Microchannels

Abstract

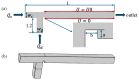
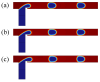
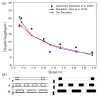
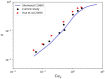
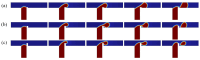
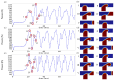
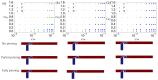
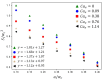
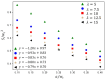
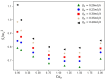
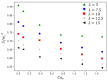
Microdroplet formation in microfluidic systems plays a pivotal role in chemical engineering, biomedicine, and energy applications. Precise control over the droplet size and formation dynamics of microdroplets is essential for optimizing performance in these fields. This work explores a hybrid control strategy that combines an active electric field with passive rib structures to regulate the droplet formation in a ribbed T-junction microchannel under an electric field. Numerical simulations based on the phase-field method are employed to analyze the effects of the electric capillary number Cae and rib height a/wc on the droplet formation mechanism. The results reveal that increasing Cae induces three distinct flow regimes of the dispersed phase: unpinning, partially pinning, and fully pinning regimes. This transition from an unpinning to a pinning regime increases the contact area between the wall and dispersed phase, restricts the flow of the continuous phase, and induces the shear stress of the wall, leading to a reduction in droplet size with the enhanced Cae. Furthermore, an increase in rib height a/wc enhances the shear stress of the continuous phase above the rib, causing a progressive shift from a fully pinning to an unpinning regime, which results in a linear decrease in droplet size. A new empirical correlation is proposed to predict droplet size S/wc2 as a function of rib height a/wc and two-phase flow rate ratio Qd/Qc: S/wc2=(-0.62-1.8Qd/Qc)(a/w)+(0.64+0.99Qd/Qc).

Keywords: electric field; microdroplet formation; microdroplet size; ribbed T-junction.

Figure 1

(a) Schematic of a ribbed T-junction microchannel under an electric field. Inlet figure: a schematic diagram of a rib with the width of b and height of a. (b) 3D schematic diagram.

Figure 2

Effect of grid size on the volume fraction of the dispersed phase: (a) grid size 9843; (b) grid size 13,105; (c) grid size 18,468.

Figure 3

Grid independence study with $Q_d=0.3$ $\mathrm{mL}/\mathrm{h}$ and $Q_c=0.9$ $\mathrm{mL}/\mathrm{h}$. $V_1$ and $V_2$ represent the velocity along the y-direction at $x=100$ $\mathsf{\mu }$m and $x=150$ $\mathsf{\mu }$m, respectively.

Figure 4

(a) Comparison of the droplet length from the experiment [20] and simulation [46] at $Q_d=0.14 \mathsf{\mu }\mathrm{L}{\mathrm{s}}^{-1}$ under different $Q_c$; (b) visualization of droplet formation from experiments [20] (left) and our simulations (right) under (I) $Q_d=0.004 \mathsf{\mu }\mathrm{L}{\mathrm{s}}^{-1}$, $Q_c=0.028 \mathsf{\mu }\mathrm{L}{\mathrm{s}}^{-1}$; (II) $Q_d=0.14 \mathsf{\mu }\mathrm{L}{\mathrm{s}}^{-1}$, $Q_c=0.139 \mathsf{\mu }\mathrm{L}{\mathrm{s}}^{-1}$; (III) $Q_d=0.111 \mathsf{\mu }\mathrm{L}{\mathrm{s}}^{-1}$, $Q_c=0.028 \mathsf{\mu }\mathrm{L}{\mathrm{s}}^{-1}$.

Figure 5

Comparison of the relationship of the deformation parameter and electrocapillary number between the current method and those of Sherwood [47] and Hua et al. [48].

Figure 6

Time evolution of the dispersed-phase volume fraction distribution at three electric capillary numbers (a) ${\mathrm{Ca}}_e=0$, (b) ${\mathrm{Ca}}_e=0.38$, and (c) ${\mathrm{Ca}}_e=1.14$, where $\mathrm{Ca}=0.036$, $Q=3$, $a/w_c=0.2$, and $b/w_c=0.3$.

Figure 7

Shear stress and streamline distribution in the microchannel, with the red line representing the isosurface of the dispersed-phase volume fraction ($\varphi =0.5$), where $\mathrm{Ca}=0.036$, $Q=3$, $a/w_c=0.2$, and $b/w_c=0.3$. ${\mathrm{Ca}}_e=0$ (up), ${\mathrm{Ca}}_e=0.38$ (middle), and ${\mathrm{Ca}}_e=1.14$ (down).

Figure 8

The variation in upstream pressure over time in the microchannel under different voltage conditions, where the dashed line represents the connection of the extreme value points, and the red dots indicate the locations of the upstream pressure points. Red markers denote measurement locations of $P_u$ and $P_d$.

Figure 9

The evolution of the channel pressure drop over time under different electric capillary numbers ($C{a}_e$) and the corresponding dispersed-phase morphology. (a,b) ${\mathrm{Ca}}_e=0$; (c,d) ${\mathrm{Ca}}_e=0.38$; (e,f) ${\mathrm{Ca}}_e=1.14$.

Figure 10

Evolution of dispersed-phase volume fraction over time for different rib heights, where $Ca=0.02$, $Q=1.67$, $C{a}_e=0.38$, and $b/w_c=0.3$. $a/w_c=0.1$ (a); $a/w_c=0.3$ (b); $a/w_c=0.5$ (c).

Figure 11

Shear stress and streamline distribution in the microchannel, with the red line representing the iso-contour of dispersed-phase volume fraction ($\varphi =0.5$), where $Ca=0.02$, $Q=1.67$, $C{a}_e=0.38$, and $b/w_c=0.3$. $a/w_c=0.1$(up); $a/w_c=0.3$ (middle); $a/w_c=0.5$ (down).

Figure 12

The graph of upstream pressure variation over time under different rib height ratios in the microchannel. The blue line represents the case of $a/w_c=0.1$; the green line represents the case of $a/w_c=0.3$; the red line represents the case of $a/w_c=0.5$.

Figure 13

The evolution of the channel pressure drop over time under different rib height ratios ($a/w_c$) and the corresponding dispersed-phase morphology. (a,b) $a/w_c=0.1$; (c,d) $a/w_c=0.3$; (e,f) $a/w_c=0.5$.

Figure 14

The flow state diagram of the dispersed phase in a T-junction microchannel with different rib height ratios and the corresponding flow behavior. (a) $a/w_c=0.1$, (b) $a/w_c=0.3$, and (c) $a/w_c=0.5$. Different symbols represent different flow states: stars (★) represent fully pinning (F), triangles (△) represent partially pinning (P), and circles (∘) represent unpinning (N).

Figure 15

The effect of rib height ratio on droplet size under different electric capillary numbers. The straight-line equation in the lower-left corner represents the fitting formula for the calculated data under different electric capillary numbers, where y represents the droplet size $S/w_c^2$ and x represents the rib height ratio $a/w_c$.

Figure 16

The effect of rib height ratio on droplet size under different dispersed-phase flow rates. The straight-line equation in the lower-left corner represents the fitting formula for the calculated data under different electric capillary numbers, where y represents the droplet size $S/w_c^2$ and x represents the rib height ratio $S/w_c^2$.

Figure 17

The effect of rib height ratio on droplet size under different viscosity ratios. The straight-line equation in the lower-left corner represents the fitting formula for the calculated data under different electric capillary numbers, where y represents the droplet size $S/w_c^2$ and x represents the rib height ratio $a/w_c$.

Figure 18

The effect of electric capillary number on droplet size at different dispersed-phase flow rates.

Figure 19

The effect of electric capillary number on droplet size at different viscosity ratios.