Detecting outbreaks using a spatial latent field
- PMID: 40743263
- PMCID: PMC12312950
- DOI: 10.1371/journal.pone.0328770
Detecting outbreaks using a spatial latent field
Abstract
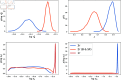
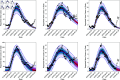
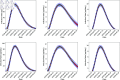
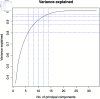
In this paper, we present a method for estimating the infection-rate of a disease as a spatial-temporal field. Our data comprises time-series case-counts of symptomatic patients in various areal units of a region. We extend an epidemiological model, originally designed for a single areal unit, to accommodate multiple units. The field estimation is framed within a Bayesian context, utilizing a parameterized Gaussian random field as a spatial prior. We apply an adaptive Markov chain Monte Carlo method to sample the posterior distribution of the model parameters condition on COVID-19 case-count data from three adjacent counties in New Mexico, USA. Our results suggest that the correlation between epidemiological dynamics in neighboring regions helps regularize estimations in areas with high variance (i.e., poor quality) data. Using the calibrated epidemic model, we forecast the infection-rate over each areal unit and develop a simple anomaly detector to signal new epidemic waves. Our findings show that anomaly detector based on estimated infection-rates outperforms a conventional algorithm that relies solely on case-counts.
Copyright: This is an open access article, free of all copyright, and may be freely reproduced, distributed, transmitted, modified, built upon, or otherwise used by anyone for any lawful purpose. The work is made available under the Creative Commons CC0 public domain dedication.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures







Similar articles
-
The effect of sample site and collection procedure on identification of SARS-CoV-2 infection.Cochrane Database Syst Rev. 2024 Dec 16;12(12):CD014780. doi: 10.1002/14651858.CD014780. Cochrane Database Syst Rev. 2024. PMID: 39679851 Free PMC article.
-
ScITree: Scalable Bayesian inference of transmission tree from epidemiological and genomic data.PLoS Comput Biol. 2025 Jun 10;21(6):e1012657. doi: 10.1371/journal.pcbi.1012657. eCollection 2025 Jun. PLoS Comput Biol. 2025. PMID: 40493703 Free PMC article.
-
Signs and symptoms to determine if a patient presenting in primary care or hospital outpatient settings has COVID-19.Cochrane Database Syst Rev. 2022 May 20;5(5):CD013665. doi: 10.1002/14651858.CD013665.pub3. Cochrane Database Syst Rev. 2022. PMID: 35593186 Free PMC article.
-
Rapid, point-of-care antigen tests for diagnosis of SARS-CoV-2 infection.Cochrane Database Syst Rev. 2022 Jul 22;7(7):CD013705. doi: 10.1002/14651858.CD013705.pub3. Cochrane Database Syst Rev. 2022. PMID: 35866452 Free PMC article.
-
Antibody tests for identification of current and past infection with SARS-CoV-2.Cochrane Database Syst Rev. 2022 Nov 17;11(11):CD013652. doi: 10.1002/14651858.CD013652.pub2. Cochrane Database Syst Rev. 2022. PMID: 36394900 Free PMC article.
References
MeSH terms
LinkOut - more resources
Full Text Sources
Medical

