Beyond Euclid: an illustrated guide to modern machine learning with geometric, topological, and algebraic structures
- PMID: 40755551
- PMCID: PMC12315666
- DOI: 10.1088/2632-2153/adf375
Beyond Euclid: an illustrated guide to modern machine learning with geometric, topological, and algebraic structures
Abstract
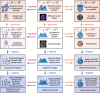
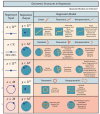
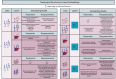
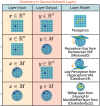
The enduring legacy of Euclidean geometry underpins classical machine learning, which, for decades, has been primarily developed for data lying in Euclidean space. Yet, modern machine learning increasingly encounters richly structured data that is inherently non-Euclidean. This data can exhibit intricate geometric, topological and algebraic structure: from the geometry of the curvature of space-time, to topologically complex interactions between neurons in the brain, to the algebraic transformations describing symmetries of physical systems. Extracting knowledge from such non-Euclidean data necessitates a broader mathematical perspective. Echoing the 19th-century revolutions that gave rise to non-Euclidean geometry, an emerging line of research is redefining modern machine learning with non-Euclidean structures. Its goal: generalizing classical methods to unconventional data types with geometry, topology, and algebra. In this review, we provide an accessible gateway to this fast-growing field and propose a graphical taxonomy that integrates recent advances into an intuitive unified framework. We subsequently extract insights into current challenges and highlight exciting opportunities for future development in this field.
Keywords: algebra; geometric deep learning; geometry; machine learning; topology.
© 2025 The Author(s). Published by IOP Publishing Ltd.
Figures







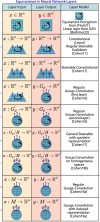
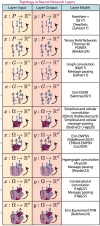

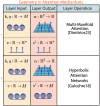


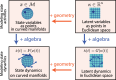
References
-
- Ahmed N K, Rossi R A, Lee J B, Willke T L, Zhou R, Kong X, Eldardiry H. Role-based graph embeddings. IEEE Trans. Knowl. Data Eng. 2022;34:2401–15. doi: 10.1109/TKDE.2020.3006475. - DOI
-
- Akhøj M, Benn J, Grong E, Sommer S, Pennec X. Principal subbundles for dimension reduction. 2023 (arXiv: 2307.03128)
-
- Alain M, Takao S, Paige B, Deisenroth M P. Gaussian processes on cellular complexes. Proc. 41st Int. Conf. on Machine Learning (ICML’24); JMLR.org; 2024.
Publication types
LinkOut - more resources
Full Text Sources
