Identification of the governing equation of stimulus-response data for run-and-tumble dynamics
- PMID: 40763301
- PMCID: PMC12338844
- DOI: 10.1371/journal.pcbi.1013287
Identification of the governing equation of stimulus-response data for run-and-tumble dynamics
Abstract
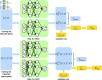
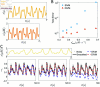
The run-and-tumble behavior is a simple yet powerful mechanism that enables microorganisms to efficiently navigate and adapt to their environment. These organisms run and tumble alternately, with transition rates modulated by intracellular chemical concentration. We introduce a neural network-based model capable of identifying the governing equations underlying run-and-tumble dynamics. This model accommodates the nonlinear functions describing movement responses to intracellular biochemical reactions by integrating the general structure of ODEs that represent these reactions, without requiring explicit reconstruction of the reaction mechanisms. It is trained on datasets of measured responses to simple, controllable signals. The resulting model is capable of predicting movement responses in more realistic, complex, temporally varying environments. Moreover, the model can be used to deduce the underlying structure of hidden intracellular biochemical dynamics. We have successfully tested the validity of the identified equations based on various models of Escherichia coli chemotaxis, demonstrating efficacy even in the presence of noisy measurements. Moreover, we have identified the governing equation of the photo-response of Euglena gracilis cells using experimental data, which was previously unknown, and predicted the potential architecture of the intracellular photo-response pathways for these cells.
Copyright: © 2025 Lei et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures


References
MeSH terms
LinkOut - more resources
Full Text Sources

