Comparison of time-of-flight and MIEZE neutron spectroscopy of H2O

Abstract

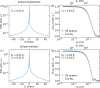
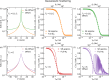
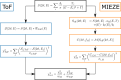
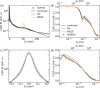
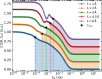
We report a comparison of modulation of intensity with zero effort (MIEZE), a neutron spin-echo technique, and neutron time-of-flight (ToF) spectroscopy, a conventional neutron scattering method. The evaluation of the respective recorded signals, which can be described by the intermediate scattering function I(Q, τ) (MIEZE) and the dynamic structure factor S(Q, E) (ToF), involves a Fourier transformation that requires detailed knowledge of the detector efficiency, instrumental resolution, signal background and range of validity of the spin-echo approximation. It is demonstrated that data obtained from pure water align well within the framework presented here, thereby extending the applicability of the MIEZE technique beyond the spin-echo approximation and emphasizing the complementarity of the two methods. Computational methods, such as molecular dynamics simulations, are highlighted as essential for enhancing the understanding of complex systems. Together, MIEZE and ToF provide a powerful framework for investigating dynamic processes across different time and energy domains, with particular attention required to ensure identical sample geometries for meaningful comparisons.

Keywords: MIEZE; data analysis; modulation of intensity with zero effort; neutron spin–echo spectroscopy; neutron time-of-flight spectroscopy.

Figure 1

Illustration of typical signals observed in MIEZE spectroscopy. The wavelength of the incoming neutron beam was assumed to be monochromatic and λ = 6.0 Å, which corresponds to E_i = 2.27 meV. (a) The dynamic structure factor described by a Lorentzian with a narrow linewidth Γ₀ = 0.01E_i, corresponding to quasielastic scattering. (b) The curve shown in panel (a) after the application of equation (9) (SE approximation, blue circles) and equation (21) (explicit calculation, solid orange line). (c) The dynamic structure factor described by a Lorentzian with a narrow linewidth Γ₀ = 0.01E_i and a small energy transfer E₀ = 0.01E_i, corresponding to low-energy inelastic scattering. (d) The curve shown in panel (c) after the application of equation (9) (SE approximation, blue circles) and equation (21) (explicit calculation, solid orange line).

Figure 2

Illustration of the difference between the SE approximation and the explicit phase calculation for quasielastic scattering. Panels (a) and (d) show two dynamic structure factors whose transformation into the time domain is shown in graphs (b) and (c), and (e) and (f), respectively, as indicated by their colour. The transformation calculated by the SE approximation is shown as circles, while the solid lines depict the result of equation (21). The wavelength of the incoming neutron beam was assumed to be monochromatic and λ = 6.0 Å, which corresponds to E_i = 2.27 meV.

Figure 3

Illustration of the difference between the SE approximation and the explicit phase calculation for inelastic scattering. Panels (a) and (d) show two dynamic structure factors whose transformation into the time domain is shown in graphs (b) and (c), and (e) and (f), respectively, as indicated by their colour. The transformation calculated by the SE approximation is shown as circles, while the solid lines depict the result of equation (21). The wavelength of the incoming neutron beam was assumed to be monochromatic and λ = 6.0 Å, which corresponds to E_i = 2.27 meV.

Figure 4

Vanadium data recorded on TOFTOF. (a) Vanadium data in energy space, shown together with a Gaussian fit to the data. (b) The data set and fit shown in panel (a) after the MIEZE transform [equation (21)] is applied.

Figure 5

Direct transformation of the recorded ToF spectra S(2ϑ = 22°, E) into the time domain. (a) The transformed ToF spectrum of FOCUS with increasing number of corrections for direct comparison with the RESEDA data (circles). The simplest case uses the SE approximation [equation (9)] and results in the blue curve. The orange curve is obtained by transforming the energy spectrum with equation (21), which reproduces quite accurately the frequency of the oscillations visible in the RESEDA data. The green line includes the energy-dependent detection efficiency of the CASCADE detector, which now gives the correct amplitude of the oscillations. Comparing this last with the MIEZE data, at high frequencies the transformed ToF data decay faster and at medium frequencies the contrast is about 0.05 lower than expected. (b) A visual­ization of the effect of adding (red line) or subtracting (purple line) a constant background to the FOCUS data before applying the trans­formation, leading to a downward or upward shift compared with the original curve, respectively. (c) A comparison of the RESEDA data (circles) with the Fourier transforms of the different ToF data sets. The data measured with the same sample cell as RESEDA (green line, measured on FOCUS) match the RESEDA data much better than the data recorded in a much thinner hollow cylinder (brown line, measured on TOFTOF), emphasizing the impact of sample thickness and multiple scattering.

Figure 6

Flow chart of fitting combined data sets. The ToF procedure is depicted using blue boxes and the MIEZE procedure is highlighted using orange ones.

Figure 7

Results of fitting the 3Q1I model. The points in blue and orange visualize measurements on the TOFTOF and RESEDA spectrometers, respectively. Where error bars are not shown, they are significantly smaller than the size of the markers. The solid lines represent the results of the fit analyses. The orange line represents the fit of the RESEDA data, convoluted with the instrument resolution for comparison with the TOFTOF data. Similarly, the blue line represents the fit of the TOFTOF data, transformed for comparison with the RESEDA data. The fit of the MIEZE data is insensitive to the inelastic scattering contribution, which is why the amplitude is overestimated to improve the fit at low energy transfers. The black line shows the result of the combined fitting. Panels (a) and (b) show the entire dynamic range of both measurements, whereas panels (c) and (d) give more detailed views of the parameter space where the SE approximation is valid.

Figure 8

Comparison of the predicted contrast calculated from the optimized 3Q1I model (Section 4.2) for data at λ_i = 4.5 Å recorded on RESEDA. The data were collected at an angle 2ϑ such that the momentum transfer Q is the same in the SE approximation. The predicted curves account for the increased integration area and the adjustments in the MIEZE phase calculation.

Figure 9

Prediction for typical data measured on RESEDA for different initial wavelengths λ_i. The purple curve corresponds to the results of fitting the TOFTOF data with model 3Q1I. This result was then used to predict MIEZE data for different wavelengths, similar to Fig. 8. The star labelled τ_min indicates the smallest Fourier time, below which the SE approximation becomes invalid, at the corresponding wavelength λ_i.