Self-sustained frictional cooling in active matter

Abstract

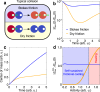
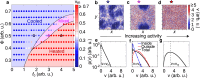
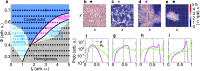
Cooling processes in nature are typically generated by external contact with a cold reservoir or bath. According to the laws of thermodynamics, the final temperature of a system is determined by the temperature of the environment. Here, we report a spontaneous internal cooling phenomenon for active particles, occurring without external contact. This effect, termed self-sustained frictional cooling, arises from the interplay between activity and dry (Coulomb) friction, and in addition is self-sustained from particles densely caged by their neighbors. If an active particle moves in its cage, dry friction will stop any further motion after a collision with a neighbor particle thus cooling the particle down to an extremely low temperature. We demonstrate and verify this self-sustained cooling through experiments and simulations on active granular robots and identify dense frictional arrested clusters coexisting with hot, dilute regions. Our findings offer potential applications in two-dimensional swarm robotics, where activity and dry friction can serve as externally tunable mechanisms to regulate the swarm's dynamical and structural properties.

Fig. 1. Self-sustained frictional cooling.

a, b Experimental setup. a 3D illustration of the active granular particle with tilted legs. b Particles are confined to an acrylic horizontal plate oscillating vertically at 110 Hz. c Illustration of self-sustained frictional cooling: initially (first image), all particles are stopped by dry friction. Occasionally, rare fluctuations in the active force initiate particle motion (highlighted in red in the second image). This motion is subsequently hindered (third image) when the moving particle collides with a neighboring particle at rest. The collision reduces the velocity of the displaced particle and allows dry friction to suppress the particle motion (fourth image). The green arrow indicates the trajectory of the moving particle, while the colliding particles are highlighted with thick black lines. d, e Experimental images for a system of active robots with packing fraction 0.45 for two different consecutive times (d initial time and e final time). Experiments are realized with shaker amplitudes of A = 18.66 ± 0.08 μm. The scale bar in the left part of panel d is equal to 15 mm (particle diameter). As the system evolves, the particles become nearly immobile, stopped by the self-sustained frictional cooling. f, g Snapshots corresponding to experimental images d-e where colors denote the instantaneous particle speed.

Fig. 2. Collisional mechanism for self-sustained frictional cooling.

a Sketch of a typical binary collision between a moving, activated particle (red) and an arrested particle (blue). A different collision scenario is predicted for Stokes and dry friction. In the latter case, both particles are arrested, while in the former case they continue moving. b, c Averaged mean kinetic energy, 〈E_kin(t)〉 (b), and center of mass of two particles (c) as a function of time t. The activated (left) particle in both cases has a typical activation speed v₀. The kinetic energy is normalized by the initial activation energy $E_{\mathrm{kin}}\left(0\right)=m{v}_0^2/2$. In both cases, after an initial drop in kinetic energy to a minimum due to the collision, the system starts to regain kinetic energy from fluctuations in the active force. d Averaged minimal kinetic energy during the cooling process as a function of activity. For low activity, dry friction cools down the system more than Stokes friction, allowing the kinetic temperature to almost approach zero. The crossover from self-sustained frictional cooling to heating is marked by a vertical dashed line dividing the activity region where cooling by dry friction becomes less effective compared to the reference system with Stokes friction. The simulation protocol to generate the elastic collisions in the case of dry friction and Stokes friction is described in the Methods.

Fig. 3. Cooled, mixed and heated phases.

a–c Snapshots at two different times to outline the time evolution of configurations for cooled (A = 18.66 ± 0.08 μm), mixed (A = 18.88 ± 0.09 μm) and heated (A = 21.56 ± 0.09 μm) phases, respectively. The snapshots in the upper row are the initial configurations, with a corresponding to that in Fig. 1g, while the lower row reports the snapshot after 30 seconds of time evolution. In the lower row, the trajectories of two highlighted tracers (one inside and one outside the cluster) are displayed for each phase. Particles with low mobility are represented by orange trajectories while those with high mobility are shown in dark green. The evolution reveals that the cluster remains stable in the cooled and mixed phases but becomes transient in the heated phase due to the significantly higher particle mobility. d–f Velocity probability distributions p(v), shown for the corresponding phases in (a)–(c). The colored solid lines represent experimental data, while the black dashed lines correspond to results obtained by simulating the dynamics (1) in a confining circular arena. Parameters of the simulations are given in Table 1. Both the cooled and mixed phases exhibit a velocity peak near zero, with the mobile particles outside the cluster in the mixed state contributing to the distribution tail at higher velocities. In contrast, the heated phase shows a complete shift of the velocity peak away from zero.

Fig. 4. Kinetic phase diagram.

a Phase diagram in the plane of reduced activity f₀ and packing fraction Φ with a color gradient denoting the mode particle speed (points). Background colors are used to distinguish between different phases: cooled (blue), mixed (pink), and heated (red) phases. The cooled phase occurs when most of the particles are frictional arrested and remain within the cluster, whereas in a heated phase, particles are highly mobile and are not significantly slowed down by the frictional forces. A state where cooled and heated phases coexist is referred to as a mixed phase. Details on the transition line between these states are discussed in the Methods. b–d Snapshots of cooled, mixed, and heated phases. The color gradient denotes the particle speed (red for high and blue for low speeds). The stars above each snapshot indicate the corresponding parameters f₀, Φ in the phase diagram a. e–g Probability distribution of the velocity p(v) for the cooled (e), mixed (f) and heated (g) phases. For the mixed state, we separately highlight the distributions for particles inside (blue) and outside (red) of the cooled cluster. Particles within the cluster exhibit characteristics of the cooled phase, while those outside behave like particles in the heated phase. In all cases p(v) exhibits a single peak v_m (dashed vertical line, mode speed), with the value of this peak depicted in the phase diagram a.

Fig. 5. Structure analysis.

a Phase diagram illustrating the four possible structural states. The thick solid lines are identical to those shown in Fig. 4. Phases are distinguished by comparing the distribution of the local packing fraction ϕ and the one of the orientational order parameter ψ₆ (see Methods for details). b, e Snapshots for the different structural phases. Particles are colored according to their speed, i.e. red and blue for high and low speed, respectively. The stars above each snapshot indicate the corresponding parameters f₀, Φ in the phase diagram a. f–i Probability distributions of the local packing fraction Prob(ϕ) (violet) and the hexagonal local order parameter Prob(ψ₆) (green). The vertical dashed lines mark the average packing fraction value Φ. The snapshots (b)–(e) correspond to the distribution (f)–(i), respectively.

Fig. 6. Schematic illustration of an active granular particle.

a Side view of the 3D-printed active granular particle, reporting heights of the particle components and the tilting angle of the legs. b Bottom view of the particle, showing the diameters of the cylinders forming the particles, the diameter of the legs, as well as the leg positions. The particle scheme is adapted from ref. .

Fig. 7. Kinetic energy relaxation.

Time evolution of the total kinetic energy $E_{\mathrm{kin}}^{\mathrm{tot}}$ for systems reaching the cooled, mixed, and heated steady-state phases. Simulations are performed under the same conditions as in Fig. 4b (cooled), c (mixed), and d (heated). These snapshots correspond to the final time frames shown in this figure. In all three cases, the kinetic energy saturates, indicating that the system has reached a steady state.