Structural stability estimated through critical perturbation determines evolutionary persistence in mutualistic model ecosystems

Abstract

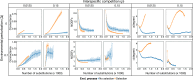
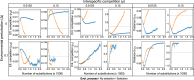
Understanding the factors that influence the persistence and stability of complex ecological networks is a central focus of ecological research. Recent research into these factors has predominantly attempted to unveil the ecological processes and structural constraints that influence network stability. Comparatively little attention has been given to the consequences of evolutionary events, despite the fact that the interplay between ecology and evolution has been recognized as fundamental to understand the formation of ecological communities and predict their reaction to change. We extend existing mutualistic population dynamical models by incorporating evolutionary adaptation events to address this critical gap. We relate ecological aspects of mutualistic community stability to the stability of persistent evolutionary pathways. Our findings highlight the significance of the structural stability of ecological systems in predicting biodiversity loss under both evolutionary and environmental changes, particularly in relation to species-level selection. Notably, our simulations reveal that the evolution of mutualistic networks tends to increase a network-dependent parameter termed critical competition, which places systems in a regime in which mutualistic interactions enhance structural stability and, consequently, biodiversity. This research emphasizes the pivotal role of natural selection in shaping ecological networks, steering them towards reduced effective competition below a critical threshold where mutualistic interactions foster stability in the face of environmental change.

Keywords: biodiversity loss; eco-evolutionary dynamics; evolutionary stability; mutualistic networks; structural stability.

Figure 1.

Eco-evolutionary model and critical competition ${\rho }_c$. (a) Schematic representation of the model. At each step of the simulation, a randomly selected species (green square) is subjected to an evolutionary event (box ‘evolutionary dynamics’). Evolutionary events are of two types: link swap (E1) or creation/loss (E2). The probabilities of events ($p$, $q$ respectively) are indicated. The effect of the event on the network is evaluated by running the ecological dynamics, where environmental perturbations may be added. Acceptance of the event depends on whether selection is considered. If selection is considered, the change is accepted only if it enhances the fitness of the modified species (i.e. there is an increase in its biomass). If there is no selection all changes are accepted, regardless of their effect on species or the community. (b) Simulated time series of species abundances illustrating the trade-off between the interspecific competition parameter $\rho$ and the critical competition ${\rho }_{\mathrm{c}}$. (c) Example of eco-evolutionary dynamics showing six trajectories for no selection (blue) and selection (orange) scenarios. The evolutionary equilibrium is achieved when no extinctions are observed throughout 350 substitutions (i.e. accepted evolutionary events). (d) log–log representation of the critical competition against the total biodiversity for a set of real plant–pollinator networks extracted from the Web of Life. The power–law relationships for both plants and animals have an exponent approximately −0.5. By means of the trade-off illustrated in (b), observing positive mutualistic effects in large communities demands decreasing the intraguild interspecific competition to favour coexistence.

Figure 2.

Structural stability explains diversity at the evolutionary equilibrium. (a) Biodiversity of the eco-evolutionary process at equilibrium for different values of the interspecific competition $\rho$ and environmental perturbation $\mathrm{\Delta }$. Each panel represents the outcome of the evolutionary process for different values of $\mathrm{\Delta }$. In boxplots, box limits represent interquartile range (IQR) and the horizontal line the median value of the final species richness ($\alpha$-diversity) across 50 simulations. Vertical lines (i.e. whiskers) show the ±1.5 IQR values. Points represent the outliers. (b) Predicted structural stability (critical environmental perturbation ${\mathrm{\Delta }}_{\mathrm{c}}$) for the starting network for each value of interspecific competition $\rho$. (c) Relationship between structural stability and final biodiversity, normalized by the starting diversity before the evolutionary process. (d) Slope of the relationship shown in (c) for different values of environmental perturbation. The closer the slope is to one the more accurate the prediction. Ordinates are not significantly different from zero for $\mathrm{\Delta }=0.1$.

Figure 3.

Disruptive evolution prompts biodiversity loss and biomass increase. Mean $\alpha$-diversity (i.e. species richness) (left), effective diversity (middle) and biomass (right) throughout eco-evolutionary trajectories (halted after stability in number of species is achieved over 350 evolutionary steps) for different values of environmental perturbation $\mathrm{\Delta }$ (rows) and interspecific competition $\rho$ (columns). Mean values (points) and standard deviation (vertical lines) are shown every 25 evolutionary steps (i.e. fixed mutation or substitutions) across 50 independent simulations for selection (orange) and no-selection (blue) scenarios.

Figure 4.

Evolution results in more connected networks that are less nested. Mean connectance (left), normalized nestedness (quantified as NODFc, middle) and standard deviation of species degrees (right) throughout eco-evolutionary trajectories (halted after stability in number of species is achieved over 350 evolutionary steps) for different values of environmental perturbation $\mathrm{\Delta }$ (rows) and interspecific competition $\rho$ (columns). Mean values (points) and standard deviation (vertical lines) are shown every 25 evolutionary steps (i.e. fixed mutation or substitutions) across 50 independent simulations for selection (orange) or no-selection (blue) scenarios.

Figure 5.

Evolution increases critical competition above effective competition. Mean effective competition ${\rho }_{\mathrm{eff}}$, critical competition ${\rho }_{\mathrm{c}}$ (middle) and their relative distance $D$ (right) throughout eco-evolutionary trajectories (halted after stability in number of species is achieved over 350 evolutionary steps) for different values of environmental perturbation $\mathrm{\Delta }$ (rows) and interspecific competition $\rho$ (columns). For reference, $\rho$ is also displayed with dotted lines in left and middle columns, and $D=0$ in the right column. Mean values (points) and standard deviation (vertical lines) are shown every 25 evolutionary steps (i.e. fixed mutation or substitutions) across 50 independent simulations for selection (orange) or no-selection (blue) scenarios. Evolution under selection always leads to systems with ${\rho }_{\mathrm{eff}}<\rho$ and ${\rho }_{\mathrm{c}}>\rho$, implying $D>0$ (${\rho }_{\mathrm{eff}}<{\rho }_{\mathrm{c}}$).

Figure 6.

Selection increases structural stability across evolutionary time. (Left) Predicted structural stability, ${\mathrm{\Delta }}_{\mathrm{c}}$, for two interspecific competition values and without environmental fluctuations (upper row) and with fluctuations of amplitude $\mathrm{\Delta }=0.1$ (lower row). (Right) Test of structural stability with simulations. Systems at steady state throughout the evolutionary simulations were tested numerically for structural stability every 25 evolutionary steps (x-axis) in the evolutionary scenarios of $\rho$ and $\mathrm{\Delta }$ combinations indicated in the right hand side. Each system was subjected to perturbations of amplitude $\mathrm{\Delta }$ (shown on the top) and their dynamics investigated. Fifty replicates of ecological dynamics, corresponding to the 50 evolutionary replicates at the corresponding evolutionary time-points (i.e. number of substitutions), were simulated for each system and amplitude, and the fraction of simulations with at least one extinction is represented in the y-axis.