Geometric principles of wobble board design for balance training and rehabilitation
- PMID: 40774976
- PMCID: PMC12331965
- DOI: 10.1038/s41598-025-07290-1
Geometric principles of wobble board design for balance training and rehabilitation
Abstract
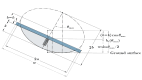
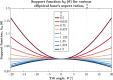
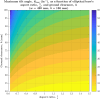
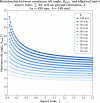
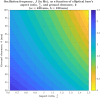
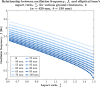
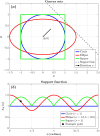
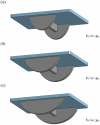
Wobble boards-unstable platforms mounted on curved bases-are widely used for balance training and rehabilitation. However, their design lacks a systematic theoretical foundation, making it difficult to precisely tailor instability characteristics to specific neuromuscular demands. This study introduces a geometric framework for optimizing wobble board instability through controlled manipulation of base geometry. We derived exact relationships between the elliptical base's geometric parameters and the board's instability characteristics for the general case of a truncated elliptical base geometry. Our analysis reveals that the ratio between the vertical and horizontal semi-axes of the elliptical base plays a critical role in shaping stability properties. If this ratio exceeds a certain critical value-which can be precisely determined from the geometry-the board transitions into an unstable regime requiring rapid, reflexive postural responses. Conversely, ratios below this critical value enable more stable configurations that support larger, compensatory movements involving gross motor coordination. The absolute size of the elliptical base further modulates these effects by scaling the overall postural demand. Furthermore, we demonstrate that ground clearance (i.e., the vertical distance between the base's truncation and the ground) governs safety trade-offs by limiting the maximum tilt angle achievable before loss of stability. These results constitute theoretical predictions derived from geometric modeling that offer a structured basis for customizing instability in training or rehabilitation contexts, though their clinical relevance remains to be established through future empirical validation. By linking these parameters to postural demands, this framework provides clinicians and trainers with a structured, evidence-based method for designing, prescribing, and progressively adapting wobble boards to match individual skill levels and neuromuscular requirements.
Keywords: Balance board; Balance control; Neuromechanics; Postural stability; Postural training; Rehabilitation engineering.
© 2025. The Author(s).
Conflict of interest statement
Declarations. Competing interests: The authors declare no competing interests.
Figures
Similar articles
-
Short-Term Memory Impairment.2024 Jun 8. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2025 Jan–. 2024 Jun 8. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2025 Jan–. PMID: 31424720 Free Books & Documents.
-
Effects of Balance Training on Balance Performance in Healthy Older Adults: A Systematic Review and Meta-analysis.Sports Med. 2015 Dec;45(12):1721-38. doi: 10.1007/s40279-015-0375-y. Sports Med. 2015. PMID: 26325622 Free PMC article.
-
Wobble Board Instability Enhances Compensatory CoP Responses to CoM Movement Across Timescales.Sensors (Basel). 2025 Jul 17;25(14):4454. doi: 10.3390/s25144454. Sensors (Basel). 2025. PMID: 40732579 Free PMC article.
-
Immunogenicity and seroefficacy of pneumococcal conjugate vaccines: a systematic review and network meta-analysis.Health Technol Assess. 2024 Jul;28(34):1-109. doi: 10.3310/YWHA3079. Health Technol Assess. 2024. PMID: 39046101 Free PMC article.
-
Sexual Harassment and Prevention Training.2024 Mar 29. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2025 Jan–. 2024 Mar 29. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2025 Jan–. PMID: 36508513 Free Books & Documents.
References
-
- Horak, F. B. Postural orientation and equilibrium: What do we need to know about neural control of balance to prevent falls?. Age Ageing35, ii7–ii11. 10.1093/ageing/afl077 (2006). - PubMed
-
- Maki, B. E. & McIlroy, W. E. The role of limb movements in maintaining upright stance: The “change-in-support’’ strategy. Phys. Therapy77(5), 488–507. 10.1093/ptj/77.5.488 (1997). - PubMed
-
- Nashner, L. M. & McCollum, G. The organization of human postural movements: A formal basis and experimental synthesis. Behav. Brain Sci.8(1), 135–150. 10.1017/S0140525X00020008 (1985).
-
- Shumway-Cook, A. Motor Control: Translating Research into Clinical Practice (Lippincoot Williams & Wilkins, Philadelphia, PA, 2007).
-
- Winter, D. A. Human balance and posture control during standing and walking. Gait Posture3(4), 193–214. 10.1016/0966-6362(96)82849-9 (1995).
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

