Mathematical modeling of dengue virus transmission: exploring vector, vertical, and sexual pathways with sensitivity and bifurcation analysis

Abstract

Background: Dengue virus (DENV) remains a critical global health threat, particularly in tropical and subtropical regions. Traditional models primarily focus on mosquito-borne transmission, overlooking alternative pathways such as vertical and sexual transmission. This study develops a comprehensive mathematical model that integrates multiple transmission routes to improve understanding of dengue dynamics and inform effective control strategies.

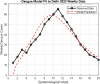
Methods: We develop a compartmental SEIR-based model that captures dengue virus transmission through mosquito vectors, vertical (transovarial), and sexual routes. The model undergoes rigorous mathematical analysis to derive equilibrium points and assess their stability. Both local and global sensitivity analyses are performed to identify key drivers of disease dynamics. Additionally, the model is calibrated using weekly dengue incidence data from Delhi, India, to validate its predictive capacity.

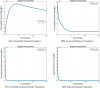
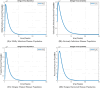
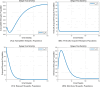
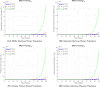
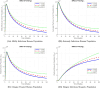
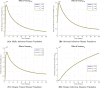
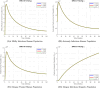
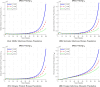
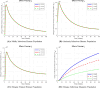
Results: The sensitivity analysis identifies the most influential parameters driving transmission. Although the human-to-human contact rate (sexual transmission) has a high sensitivity index, the actual contribution of sexual transmission to the basic reproduction number () is biologically negligible—approximately 0.01704 out of a total of 0.02, i.e., less than 1%. In contrast, mosquito-borne transmission remains the dominant route. The vaccination rate exhibits a negative sensitivity index, indicating its suppressive impact on disease spread. Numerical simulations reveal that dengue can persist even when , indicating backward bifurcation, which necessitates enhanced intervention strategies beyond just reducing .

Conclusion: The model reveals that dengue can persist even when , due to backward bifurcation. Although sexual transmission contributes less than 1% to under current estimates, vector control and vaccination remain the most critical strategies. Incorporating climate and mobility dynamics in future studies can further enhance model accuracy and policy relevance.

Keywords: Dengue intervention strategies; Epidemiological modeling; Human-to-human transmission; Mosquito-to-mosquito transmission; Vector-borne infections.

Fig. 1

Dengue Model Flow Diagram, Bifurcation Diagram, Local and PRCC Global Sensitivity Bars. A This subfigure illustrates the dengue virus transmission model, showing the interactions between different compartments in both the human and mosquito populations. The human population is categorized into susceptible, vaccinated, vertically exposed, exposed, mildly infectious, seriously infectious, treated, and recovered individuals. The mosquito population is divided into susceptible, vertically exposed, exposed, and infectious mosquitoes. The diagram includes multiple transmission pathways: vector-borne (mosquito-to-human and human-to-mosquito), vertical (mother-to-child in both humans and mosquitoes), and sexual transmission (human-to-human). Arrows represent transitions between compartments, governed by infection, recovery, vaccination, and natural death processes. B This subfigure presents the bifurcation analysis of the dengue virus model, revealing the occurrence of backward bifurcation. It plots the basic reproduction number () against disease prevalence, demonstrating that dengue can persist even when . The coexistence of both the disease-free and endemic equilibria suggests that standard control measures might not be sufficient for complete disease eradication, emphasizing the need for aggressive intervention strategies. C This subfigure depicts the sensitivity analysis of key model parameters affecting dengue transmission. It identifies the most influential factors contributing to disease spread, such as the mosquito biting rate, human-to-human transmission rate, and recovery rates. The analysis provides insights into which parameters should be prioritized in public health interventions, such as vector control and vaccination efforts. D This subfigure presents the Partial Rank Correlation Coefficient (PRCC) analysis, which quantifies the influence of different parameters on the basic reproduction number (). The x-axis represents PRCC values, indicating the strength and direction of each parameter’s effect on dengue transmission. The y-axis lists the model parameters, including mosquito biting rate (), human-to-human transmission rate (), recovery rates (), and vaccination rate (). Positive PRCC values indicate parameters that enhance disease transmission, while negative values highlight factors that help reduce it. This analysis is crucial for identifying priority targets in dengue control strategies, including mosquito control, vaccination, and treatment programs

Fig. 2

Simulation Results of Susceptible, Vaccinated, Vertically Exposed and Exposed Human Populations. A This subfigure presents the simulation of the susceptible human population over time. It illustrates the decline in susceptibility due to interactions with infected individuals, vaccination efforts, and vertical transmission. The susceptible population decreases as individuals become exposed through infection, receive vaccination, or transition to other compartments in the model. The rate of decline depends on factors such as mosquito biting rate, infection probability, and vaccination coverage. B This subfigure shows the trend of the vaccinated human population under the model’s assumptions. The number of vaccinated individuals increases as susceptible individuals receive the dengue vaccine, but it may decline over time due to waning immunity or individuals moving into exposed or infectious compartments. The curve reflects the impact of vaccination strategies in controlling the spread of dengue and reducing the pool of susceptible individuals. C This subfigure captures the dynamics of vertically exposed individuals—newborns who acquire dengue virus from their infected mothers. The population of vertically exposed individuals fluctuates based on the rate of vertical transmission, birth rates, and transition into infectious or recovered states. This simulation highlights the contribution of maternal transmission to dengue persistence and the potential need for interventions targeting pregnant women. D This subfigure represents the exposed human population, consisting of individuals who have been infected but are not yet infectious. The growth and decline of this group are influenced by infection rates, incubation periods, and transitions to symptomatic (infectious) stages. The curve illustrates the latent phase of dengue infection, where individuals do not transmit the virus but will eventually contribute to disease spread upon entering the infectious stage

Fig. 3

Simulation Results of Mildly Infectious, Seriously Infectious, Dengue Treated and Dengue Recovered Human Populations. A This subfigure presents the simulation of the mildly infectious human population over time. It represents individuals who are infected but experience mild symptoms. The population of this compartment varies based on the rate of exposure, progression to serious infection, treatment-seeking behavior, and recovery rates. The curve highlights the transient nature of mild infections and their role in disease spread. B This subfigure illustrates the seriously infectious human population, which includes individuals experiencing severe symptoms of dengue. The curve reflects the progression from the exposed or mildly infectious stages to serious infection and accounts for disease mortality, treatment, and recovery rates. The trends in this population help assess the potential burden on healthcare systems. C This subfigure depicts the population of individuals receiving proper treatment for dengue infection. The movement into this compartment depends on the rate at which infected individuals seek treatment, healthcare availability, and effectiveness of medical interventions. The population size changes based on the recovery rate, natural mortality, and disease-related deaths. D This subfigure shows the dengue recovered human population, representing individuals who survive the infection and gain immunity (either temporary or permanent). The population trends are influenced by recovery rates, reinfection risks, and potential transition to the vaccinated compartment. Understanding this curve is essential for estimating long-term immunity and reinfection risks

Fig. 4

Simulation Results of Susceptible, Vertically Exposed, Exposed and Infectious Mosquito Populations. A This subfigure presents the simulation of the susceptible mosquito population over time. It represents the population of mosquitoes that have not yet been exposed to the dengue virus. The changes in this population are influenced by birth rates, natural mortality, and the rate of infection from human-to-mosquito transmission. The decline in susceptible mosquitoes is driven by their transition to the exposed compartment after biting an infectious human. B This subfigure illustrates the vertically exposed mosquito population, which consists of mosquitoes that inherit dengue virus from infected mother mosquitoes through transovarial transmission. The number of vertically exposed mosquitoes depends on the rate of vertical transmission, mosquito birth rates, and the transition to the exposed or infectious state. This pathway contributes to dengue persistence in the environment. C This subfigure depicts the exposed mosquito population, which consists of mosquitoes that have acquired the virus but are not yet infectious. The incubation period in this compartment is crucial because these mosquitoes will eventually transition into the infectious stage. The increase in this population depends on the mosquito biting rate and transmission efficiency, while the decline is influenced by progression to the infectious state and natural mosquito mortality. D This subfigure presents the infectious mosquito population, representing mosquitoes that have completed the incubation period and are now capable of transmitting the dengue virus to humans. The size of this population is influenced by the rate at which exposed mosquitoes become infectious, mosquito lifespan, and control measures such as insecticides and environmental interventions. This population plays a critical role in sustaining dengue transmission in the environment

Fig. 5

Simulation Results of Varying the Mosquito-to-human Transmission Rate Parameter . A This subfigure presents the simulation results of the mildly infectious human population under varying mosquito-to-human transmission rate (). It shows how changes in this parameter influence the number of individuals with mild symptoms over time. The population dynamics depend on infection rates, recovery rates, and progression to serious infection. The curve highlights the role of mosquito bites in sustaining mild infections. B This subfigure illustrates the impact of varying mosquito-to-human transmission rate () on the seriously infectious human population**. It shows how an increase in transmission leads to higher cases of severe dengue infections, affecting hospitalization and potential mortality. The dynamics depend on progression from mild infection, treatment-seeking behavior, and fatality rates. C This subfigure depicts the treated human population, showing how changes in mosquito-to-human transmission rate () influence the number of individuals receiving treatment. The population size varies based on treatment rates, recovery rates, and access to healthcare services. The curve helps assess the effectiveness of medical interventions in controlling severe dengue cases. D This subfigure presents the dynamics of the infectious mosquito population under varying mosquito-to-human transmission rate (). The number of infectious mosquitoes is affected by human-to-mosquito infection rates, mosquito lifespan, and environmental conditions. The simulation highlights the role of vector control strategies in reducing the spread of dengue

Fig. 6

Simulation Results of Varying the Human-to-human Transmission Rate Parameter . A This subfigure presents the simulation results of the mildly infectious human population under varying human-to-human transmission rate (). The curve illustrates how changes in direct human transmission impact the spread of mild dengue infections. The population dynamics depend on exposure rate, progression to serious infection, recovery rate, and human contact behavior. B This subfigure demonstrates the influence of human-to-human transmission rate () on the seriously infectious human population. A higher transmission rate leads to an increase in severe dengue cases, affecting hospitalizations and mortality. The dynamics are shaped by disease severity, treatment access, and mortality risks. C This subfigure represents the dengue treated human population, showing how varying human-to-human transmission rate () affects the number of individuals receiving medical treatment. The population size is influenced by treatment-seeking behavior, healthcare availability, and recovery rates. D This subfigure presents the infectious mosquito population, highlighting the impact of human-to-human transmission rate () on mosquito infection dynamics. The curve reflects the role of human cases in sustaining mosquito infection cycles, influenced by mosquito biting rates, environmental factors, and control strategies

Fig. 7

Simulation Results of Varying the Human-to-Mosquito Transmission Rate Parameter . A This subfigure presents the simulation results of the mildly infectious human population under varying human-to-mosquito transmission rate (). The curve illustrates how changes in the rate of human-to-mosquito transmission impact the number of mildly infectious individuals. The population dynamics depend on mosquito biting rate, exposure rate, recovery rate, and treatment-seeking behavior. B This subfigure demonstrates the influence of human-to-mosquito transmission rate () on the seriously infectious human population. A higher transmission rate leads to an increase in severe dengue cases, affecting hospitalizations and mortality. The trends in this population highlight the need for effective vector control strategies. C This subfigure represents the dengue treated human population, showing how varying human-to-mosquito transmission rate () affects the number of individuals receiving medical treatment. The size of this population depends on access to treatment, disease severity, and healthcare efficiency. The results help assess the effectiveness of treatment in mitigating the impact of dengue. D This subfigure presents the dynamics of the infectious mosquito population, highlighting the impact of human-to-mosquito transmission rate () on mosquito infection levels. The curve reflects the rate at which infected humans contribute to mosquito infections, influenced by biting rates, environmental factors, and vector control measures

Fig. 8

Simulation Results of Varying the Mosquito-to-mosquito Transmission Rate Parameter . A This subfigure presents the simulation results of the mildly infectious human population under varying mosquito-to-mosquito transmission rate (). The curve illustrates how the spread of infection among mosquitoes affects the number of mildly infectious humans. The population dynamics depend on vector transmission efficiency, mosquito biting rate, and human recovery rates. B This subfigure demonstrates the impact of mosquito-to-mosquito transmission rate () on the seriously infectious human population. A higher mosquito-to-mosquito transmission rate increases the overall mosquito infection burden, which in turn raises the number of severe human cases. The trends highlight the indirect role of mosquito population dynamics in shaping dengue severity in humans. C This subfigure represents the dengue treated human population**, showing how changes in mosquito-to-mosquito transmission rate () influence the number of individuals receiving medical treatment. The population size varies based on disease severity, treatment-seeking behavior, and healthcare availability. Understanding this relationship helps assess the potential burden on medical facilities. D This subfigure presents the infectious mosquito population, highlighting the role of mosquito-to-mosquito transmission rate () in sustaining dengue transmission. The number of infectious mosquitoes depends on vertical transmission, mosquito lifespan, and external factors like environmental conditions and control measures. Effective vector control strategies can significantly reduce the infectious mosquito population and curb disease spread

Fig. 9

Simulation Results of Varying the Dengue Treated Disease Death Rate Parameter . A This subfigure presents the simulation results of the **mildly infectious human population under varying dengue treated disease death rate (). It demonstrates how changes in mortality among treated individuals influence the number of mildly infectious individuals over time. The population dynamics depend on treatment accessibility, disease progression, and healthcare interventions. B This subfigure illustrates the impact of dengue treated disease death rate () on the seriously infectious human population. A higher mortality rate among treated individuals may lead to increased disease burden, affecting hospitalization rates and overall survival. The curve helps assess the importance of early intervention and improved medical care. C This subfigure represents the dengue treated human population, showing how changes in influence the number of individuals receiving medical treatment. The population size is influenced by treatment success rates, disease severity, and healthcare system efficiency. The results provide insights into healthcare policy effectiveness in reducing severe dengue outcomes. D This subfigure presents the infectious mosquito population, demonstrating the indirect effects of human mortality () on mosquito infection dynamics. A higher mortality rate among treated individuals may alter the infection transmission cycle, affecting human-to-mosquito interactions. The trends emphasize the importance of human survival in controlling mosquito infection levels

Fig. 10

Simulation Results of Varying the Mosquito Dengue Disease Death Rate Parameter . A This subfigure presents the simulation results of the mildly infectious human population under varying mosquito dengue disease death rate (). The curve illustrates how changes in mosquito mortality due to dengue infection influence the number of mildly infectious individuals. The population dynamics depend on mosquito lifespan, transmission efficiency, and human infection rates. B This subfigure demonstrates the impact of mosquito dengue disease death rate () on the seriously infectious human population. A higher mosquito mortality rate due to dengue reduces overall mosquito infectivity, potentially lowering the number of severe human infections. The trends highlight the role of mosquito survival in disease transmission. C This subfigure represents the dengue treated human population, showing how changes in affect the number of individuals receiving medical treatment. The population size is influenced by disease burden, mosquito control strategies, and access to healthcare services. The results provide insights into the effectiveness of vector control in reducing treatment demands. D This subfigure presents the infectious mosquito population, highlighting the impact of mosquito dengue disease death rate () on the mosquito-to-human transmission cycle. The curve reflects how higher mosquito mortality rates due to dengue infection affect the spread of the virus. Effective vector control measures, such as insecticide use and habitat reduction, can significantly decrease the number of infectious mosquitoes, limiting disease transmission

Fig. 11

Comparison of predicted dengue cases from the model with observed weekly incidence data from Delhi, India (2023)