Dynamics analysis of a cam with flat-bottomed follower system

Abstract

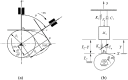
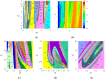
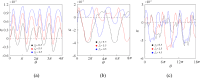
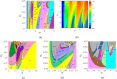
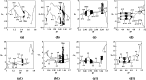
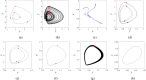
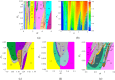
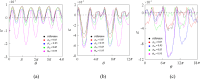
In response to the problem that the dynamic error caused by the elasticity of the follower rod should be taken into account when designing the cam profile, the form of contact between the cam and the follower rod is chosen in the paper as nonlinear Hertzian elastic contact. In order to obtain the expected movement of the follower rod, the dynamics of the system in the two-parameter planes of [Formula: see text], [Formula: see text] and [Formula: see text] are calculated to reveal the stable operation interval, the range of failure, and the reasonable parameter combinations. The transmigration processes between the movements n-p and n-(p + 1), n-p and (n + 1)-p as well as n-p and (n + 1)-(p + 1) and some special districts induced by them are discussed. Bifurcation diagrams, phase diagrams, and mapping diagrams are used to fully reveal the correlation between cam rotational speed, pressure, nonlinear contact stiffness, and contact damping and the dynamic performance of the system, while comparing the contact force as well as the depth of intrusion at various stages of the cam input curve. It is shown that the detachment of the cam and the follower rod mainly occurs at the beginning of far dwell phase and when the descent travel turns to the near dwell phase.

Keywords: Cam; Detachment; Flat-bottomed follower; Hertzian contact; Nonlinear dynamics.

Fig. 1

Schematic diagram of a cam with flat-bottomed follower system. (a) Input curve of the cam. (b) Mechanical model.

Fig. 2

Distribution pattern and bifurcation characteristics of the separation motion of the follower from the cam in the -plane, where the two parameters, i.e., cam rotation speed and preload force are varied simultaneously. (a) global distribution of n-p periodic movements. (b) duty cycle distribution. (c) district of distribution for fundamental periodic movements 1-p in the low-speed district. (d) translational domains of periodic movements 1–1 vs. 2–2. (e) translational domains of neighboring periodic movements n-p vs. (n + 1)-(p + 1).

Fig. 3

Displacement changes of the follower and the cam corresponding to three sets of pressure at different rotational speeds. (a) . (b) . (c) .

Fig. 4

Distribution pattern and bifurcation characteristics of the separation motion of the follower from the cam in the -plane, where the two parameters, i.e., cam rotation speed and contact stiffness ratio are varied simultaneously. (a) global distribution of n-p periodic movements. (b) duty cycle distribution. (c) the group of periodic movements 1-p distribution district. (d) translational process of periodic movements 1–1 vs. 2 − 1. (e) translational.

Fig. 5

Bifurcation diagrams of number of periods and number of detachments for the variation of a single parameter when takes different values. (a, a1) . (b, b1) . (c, c1) . (d, d1) .

Fig. 6

Phase diagram and Poincaré mapping of periodic movement transitions and quasi-periodic movement under . (a) 3 − 2 movement at . (b) chaos at . (c) Poincaré mapping of chaos at . (d) 4–4 movement at . (e) 2–2 movement at . (f) 1–1 movement at . (g) quasi-periodic movement at . (h) Poincaré mapping of quasi-periodic movement at .

Fig. 7

Distribution pattern and bifurcation characteristics of the separation motion in the -plane, where the two parameters, i.e., cam rotation speed and contact damping ratio are varied simultaneously. (a) global distribution of periodic movements n-p. (b) duty cycle distribution. (c) fundamental periodic movement 1-p distribution district. (d) translational processes of neighboring periodic movements n-p and (n + 1)-(p + 1) (n = p). (e) translational process of periodic movements 2 − 1 vs. 3–3.

Fig. 8

Displacement variations between the cam and the follower corresponding to different stiffness ratios and damping ratios at different speeds when . (a) . (b) . (c) .

Fig. 9

Contact forces corresponding to different speeds when . (a) . (b) . (c) .