Cahn-Hilliard dynamical models for condensed biomolecular systems

Abstract

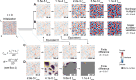
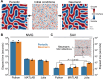
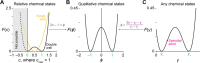
Biomolecular condensates create dynamic subcellular compartments that alter systems-level properties of the networks surrounding them. One model combining soluble and condensed states is the Cahn-Hilliard equation, which specifies a diffuse interface between the two phases. Customized approaches required to solve this equation are largely inaccessible. Using two complementary numerical strategies, we built stable, self-consistent Cahn-Hilliard solvers in Python, MATLAB, and Julia. The algorithms simulated the complete time evolution of condensed droplets as they dissolved or persisted, relating critical droplet size to a coefficient for the diffuse interface in the Cahn-Hilliard equation. We applied this universal relationship to the chromosomal passenger complex, a multi-protein assembly that reportedly condenses on mitotic chromosomes. The fully constrained Cahn-Hilliard simulations yielded dewetting and coarsening behaviors that closely mirrored experiments in different cell types. The Cahn-Hilliard equation tests whether condensate dynamics behave as a phase-separated liquid, and its numerical solutions advance generalized modeling of biomolecular systems.

Keywords: CPC; HeLa; MCF10A; Phase separation; cancer; multigrid; scalar auxiliary variables.

Figure 1.. Practical simulations of the Cahn-Hilliard equation require customized solvers

(A and B) Time evolution of spinodal decomposition solved by nonlinear multigrid (A) or scalar auxiliary variables (B) over 1.1e-2 characteristic times ($t_{\mathit{char}}$) defined by the length of $\mathrm{X}$ and $\mathrm{Y}$ spatial domains ($L_X,L_Y$) and system diffusivity ($D$). Both solvers used a 5.5e-6 time step ($dt$) defined by the mesh size in $X$ and $Y(dx,dy$) and $D$. (C) Time evolution for the same spinodal decomposition solved by finite difference using a 100-fold smaller $dt$ (5.5e-8) for 1% of the duration in (A) and (B). (D) Numerical instabilities triggered by the finite difference solver when using a 10-fold smaller $dt$ (5.5e-7) than in (A) and (B). Defects appear as checkerboards in the mesh (inset) and become undefined (gray). Simulations were initialized as a random mixture of ±1 chemical states on a 2⁷ square mesh and smoothed before iterating with Neumann boundary conditions (STAR Methods). Alternative initializations and boundary conditions are shown in Figure S1. See also Figure S1.

Figure 2.. Computing performance depends on the programming language for NMG and the boundary condition for SAV.

(A) Snapshots of spinodal decomposition when boundary conditions are periodic (left), whereby flux exiting one edge enters on the opposite edge, or Neumann (right) specifying zero flux at the edges. (B and C) Runtime performance for NMG (B) and SAV (C) solvers in Python, MATLAB, and Julia for spinodal decompositions initialized with N = 3 random mixtures of ±1 chemical states (25:75, 50:50, and 75:25) and either periodic or Neumann boundary conditions. For SAV, Neumann boundary conditions require $X$ and $Y$ reflections to re-establish periodic boundaries for the expanded spatial domain (C, inset). Boundary conditions in (C) were tested by multiway ANOVA with boundary condition and programming language as factors. All simulations were performed on a Linux x86_64 processor with 100 GB RAM on a 2⁷ × 2⁷ mesh ($L_X=L_Y=1$) for 2000 time steps ($dt=5.5\mathrm{e}-6$) and ${ϵ}_{m=8}$. See also Figure S2.

Figure 3.. Multithreaded Cahn-Hilliard simulations define the relationship between ϵm and critical droplet radii.

(A) Simulated dynamics for two normalized initial droplet radii ($R_0$) on a 2⁸ × 2⁸ mesh ($L_x=L_y=1$) for 400,000 time steps ($dt=2.5\mathrm{e}-5$) and ${ϵ}_{m=12}\approx 0.011$. The interface between the circular droplet and soluble phase was initialized to the hyperbolic tangent for an infinite interface (Box 2 and STAR Methods). The proportion of $R_0=0.09$ relative to $R_0=0.12$ is shown for each characteristic time point ($t_{\mathit{char}}$). (B) Scan of $R_0$ to determine the critical initial radius ($R_i$) and the critical equilibrium radius ($R_{eq}$) for a given ${ϵ}_m$. $R_i$ was calculated at $t=0$ between the largest $R_0$ that dissolves away (yellow) and the smallest $R_0$ that persists (marigold). $R_{eq}$ was estimated from the inflection point of the largest dissolving droplet (STAR Methods). (C) Enlargement of the first 0.1% of the time simulated in (C). (D and E) Calculation of $R_i$ (D) and $R_{eq}$ (E) as in (B) from ${ϵ}_{m=4}$ on a 2⁸ × 2⁸ mesh (= 0.0037) to ${ϵ}_{m=48}$ on a 2⁷ × 2⁷ mesh (= 0.0901). Calculations for ${ϵ}_{m=\mathrm{8,12,16}}$ on a 2⁸ × 2⁸ mesh (triangles) were repeated for ${ϵ}_{m=\mathrm{4,6},8}$ on a 2⁷ × 2⁷ mesh (circles) to confirm overlap. In (D), calculations are compared to a prior theory (inset) relating $R_i$ and ${ϵ}_m$; systematic deviations are indicated in blue. In (E), calculations are compared to a hyperbolic-to-linear fit (inset); goodness-of-fit was 0.997. The approximate condition in (B) is highlighted (yellow box). See also Figure S3.

Figure 4.. Chromatin-bound foci outside the inner centromere (IC) define a critical equilibrium radius (Req) for the chromosomal passenger complex (CPC).

(A) CPC recruitment to the IC during prophase and prometaphase. Freely diffusible CPC (green) and chromatin bound CPC is recruited strongly to the IC between kinetochores (magenta) and less so between sister chromatids. During late prophase, CPC dewets into discrete foci, which coarsen until all CPC is IC-localized by prometaphase. (B) Immunofluorescence illustration of CPC dewetting on a HeLa chromosome stained for AURKB (a CPC subunit; green), anti-centromeric antigen (ACA; magenta), and DAPI to label DNA (blue). ACA labeling of kinetochores distinguishes IC foci (orange) and non-IC foci (gray) of CPC during quantification (STAR Methods). (C) Histogram of non-IC foci (gray) and IC foci (white and orange) quantified by idealized circular radius from N = 221 chromosomes in 10 HeLa cells. The 95th percentile of the non-IC droplet size distribution defining $R_{eq}$ is shown. The distribution of non-IC foci (N = 321) and IC foci (N = 195) were compared by KS test. (D) Estimation of ${ϵ}_m$ from measured $R_{eq}$ using the hyperbolic-to-linear regression (Figure 3E) scaled for a 3200-nm physical spatial domain. The interquartile range (IQR) was calculated by 50% subsampling of N = 10 HeLa cells for 100 iterations without replacement and propagating to the ${ϵ}_m$ estimate. See also Figure S4.

Figure 5.. Cahn-Hilliard simulations predict extended multi-droplet regimes for physical values of CPC inner centromere radius (RIC)andpH3T3width(W).

(A–D) Dynamics at 1, 2, 3, and 4% $t_{\mathit{char}}$ (corresponding to the indicated time in minutes based on chromatin diffusivity and mesh size; Equation 11) for $W=60\text{nm}$ (A, B) or 90 nm (C, D) and $R_{IC}$ = 350 nm (A, C) or 120 nm (B, D). Sustained droplets are highlighted in (C) and (D) (yellow). (E–H) Dynamics at 10, 20, 30, and 40% $t_{\mathit{char}}$ for $W=120\text{nm}$ (E, F) or 140 nm (G, H) and $R_{IC}=350\text{nm}$ (E, G) or 120 nm (F, H). Sustained droplets (asterisks) are described further in Figure S5. Droplet patterns are representative for the intervals of $W$ listed on the left. All simulations were performed on a Linux x86_64 processor with 200 GB RAM on a 2⁹ × 2⁹ mesh ($L_x=L_y=2$) for 26,214 (A–D) or 262,144 (E–H) time steps ($dt=1.53\mathrm{e}-6$). See also Figure S5.

Figure 6.. Chromatin-bound CPC behaves as a phase-separated Cahn-Hilliard fluid

(A and B) Kymogram illustration of central droplets for 6.8 minutes after initialization with $R_{IC}=150\mathrm{nm}$ and $W=90\mathrm{nm}$ (A) or 90 ± 10 nm (B, white arrows). Drop-to-drop distances were quantified at randomly selected times t. (C) Immunofluorescence staining of dewetted CPC on HeLa chromosomes after G2 release for 10 minutes. (D) Normalized intensity of AURKB and ACA for the HeLa chromosome in (C). (E) Comparison of bootstrapped peak-to-peak separation of CPC foci in HeLa cells (gray histogram) with drop-to-drop distances from Cahn-Hilliard simulations with ${ϵ}_m=21.6\mathrm{nm}$ (red line). (F) Immunofluorescence staining of dewetted CPC on MCF10A-5E chromosomes after G2 release for 70 minutes. (G) Normalized intensity of AURKB and ACA for the MCF10A-5E chromosome in (G). (H) Comparison of bootstrapped peak-to-peak separation of CPC foci in MCF10A-5E cells (gray histogram) with drop-to-drop distances from Cahn-Hilliard simulations with ${ϵ}_m=28.5\mathrm{nm}$ (red line). For (C) and (F), cells were stained for AURKB (a CPC subunit; green), anti-centromeric antigen (ACA; magenta), and DAPI to label DNA (blue). A 300-nm thick axial line scan (dotted yellow line) was used to identify peaks of AURKB foci (yellow triangles; STAR Methods). For (D) and (G), normalized fluorescence intensities are shown relative to distance from the inner centromere based on the peak ACA location centered at zero. Peaks of AURKB foci (yellow triangles) were identified with a computational algorithm (STAR Methods) and quantified. For (E) and (H), data are shown as the median ± 95% bootstrapped confidence interval (CI) from N = 221 chromosomes in 10 cells (E) or 216 chromosomes in 50 cells (H). The fraction of predicted (red) and measured (black) separations greater than 1.5 μm is indicated. See also Figure S6.

Figure. B1.. The Cahn-Hilliard double-well free energy function (F) accommodates differences in location and scale

(A) Comparison of a single-well function (yellow, with $c_{\mathit{avg}}=0.5$) and a double-well function (black, stable states at 0 and 1 in green). (B) The double-well function of (A) is made symmetric about the y-axis with linear shifts and scaling (purple). (C) Any pair of chemical states (${\gamma }_{-}$ and ${\gamma }_{+}$ in green) is similarly shifted and scaled to (B). The spinodal point (magenta) is constrained.