Enhancing genome-scale metabolic models with kinetic data: resolving growth and citramalate production trade-offs in Escherichia coli

Abstract

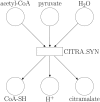
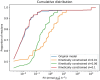
Summary: Metabolic models are valuable tools for analyzing and predicting cellular features such as growth, gene essentiality, and product formation. Among the various types of metabolic models, two prominent categories are constraint-based models and kinetic models. Constraint-based models typically represent a large subset of an organism's metabolic reactions and incorporate reaction stoichiometry, gene regulation, and constant flux bounds. However, their analyses are restricted to steady-state conditions, making it difficult to optimize competing objective functions. In contrast, kinetic models offer detailed kinetic information but are limited to a smaller subset of metabolic reactions, providing precise predictions for only a fraction of an organism's metabolism. To address these limitations, we proposed a hybrid approach that integrates these modeling frameworks by redefining the flux bounds in genome-scale constraint-based models using kinetic data. We applied this method to the constraint-based model of Escherichia coli, examining both its wild-type form and a genetically modified strain engineered for citramalate production. Our results demonstrate that the enriched model achieves more realistic reaction flux boundaries. Furthermore, by fixing the growth rate to a value derived from kinetic information, we resolved a flux bifurcation between growth and citramalate production in the modified strain, enabling accurate predictions of citramalate production rates.

Availability and implementation: The Python code generated for this work is available at: https://github.com/jlazaroibanezz/citrabounds.

Figure 1.

Petri net modeling the citramalate synthesis reaction specified in Equation (2). Metabolites are modeled by places, which are depicted as circles, and reactions are modeled by transitions, which are depicted as rectangles.

Figure 2.

(a) Growth rate (blue line, triangle points) and number of dormant reactions (red line, round points) with uncertainty parameter $d=0.01$ as the number of implemented kinetic bounds increases, (b) with uncertainty parameter $d=0.06$ and (c) with uncertainty parameter $d=0.1$. (d) Number of reactions with more variability (blue line, triangle points) and number of reactions with less variability (orange line, round points) with respect to the original model as the number of implemented kinetic bounds increases with d = 0.01, (e) with d = 0.06, and (f) with d = 0.1.

Figure 3.

Cumulative distribution of FV(r) values in the original model (blue curve) and in the constraint-based model after the kinetic bounds for all reactions were added (kinetically constrained model) with d = 0.01 (orange curve), d = 0.06 (green curve), and d = 0.1 (red curve).

Figure 4.

Simplified Petri net depicting the location of bifurcation (cyan arrows) between growth and citramalate production. Cyan arrows indicate where the bifurcation of fluxes occurs. Reactions with numbers (1), (2), and (3) represent the reactions CitraTransp1, CitraTransp2, and EX_Citramalate, respectively, added to the constraint-based model so that citramalate can leave the system. For simplicity, some places were not represented so their corresponding arrows point no element. The “…” means that more metabolites are involved in the reaction where they appear: if “…” appears next to an incoming arc, there are more reactants in that reaction; if “…” is next to an outgoing arc, more products take part in that reaction although not depicted.

Figure 5.

(a) Dormant reactions (red line, round points) and citramalate production flux (blue line, triangle points) in the citramalate-producing model as the number of implemented kinetic bounds increases when $d=0.1$, (b) when $d=0.3$, and (c) when $d=0.5$. Number of reactions with more variability (blue line, triangle points) and number of reactions with less variability (orange line, round points) in the citramalate-producing model with respect to the original model as the number of implemented kinetic bounds increases for (d) $d=0.1$, (e) $d=0.3$, and (f) $d=0.5$.

Figure 6.

Cumulative distribution of FV(r) values in the enriched original model (blue curve) and in the constraint-based model after the kinetic bounds for all reactions were added (kinetically constrained model) with d = 0.1 (red curve), d = 0.3 (green curve), and d = 0.5 (orange curve).