Burst estimation through atomic decomposition (BEAD): A toolbox to find oscillatory bursts in brain signals

Abstract

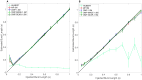
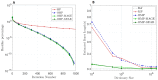
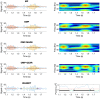
Recent studies have shown that brain signals often show oscillatory bursts of short durations, which have been linked to various aspects of computation and behavior. Traditional methods often use direct spectral estimators to estimate the power of brain signals in spectral and temporal domains, from which bursts are identified. However, direct spectral estimators are known to be noisy, such that even stable oscillations may appear bursty. We have previously shown that the Matching Pursuit (MP) algorithm, which uses a large overcomplete dictionary of basis functions (called "atoms") to decompose the signal directly in the time domain, partly addresses this concern and robustly finds long bursts in synthetic as well as real data. However, MP is a greedy algorithm that can give non-optimal solutions and requires a large-sized dictionary. To address these concerns, we extended two other algorithms-orthogonal MP (OMP) and OMP using Multiscale Adaptive Gabor Expansion (OMP-MAGE), to perform burst duration estimation. We also develop a novel algorithm, called OMP using Gabor Expansion with Atom Reassignment (OMP-GEAR). These algorithms overcome the limitations of MP and can work with a significantly smaller dictionary size. We find that, in synthetic data, OMP, OMP-MAGE, and OMP-GEAR converge faster than MP. Also, OMP-MAGE and OMP-GEAR outperform both MP and OMP when the dictionary size is small. Finally, OMP-GEAR significantly outperforms OMP-MAGE when the bursts are overlapping. Importantly, the burst durations obtained using MP and OMP with a very large-sized dictionary are comparable with that obtained using OMP-MAGE with a much smaller-sized dictionary in real data obtained from two monkeys passively viewing static gratings which induced gamma bursts in the primary visual cortex. OMP-GEAR yields slightly smaller burst durations, but all the estimated burst durations are still significantly larger than the duration estimated using traditional methods. These results suggest that gamma bursts are longer than previously reported. Raw data from two monkeys, as well as codes for both traditional and new methods, are publicly available as part of this toolbox.

Keywords: burst detection; compressed sensing; gamma; local field potential; matching pursuit; overcomplete representations.

Fig. 1.

Comparison of gamma duration estimators. (A) Injected versus estimated burst lengths, when the injected burst has one-fourth the power of the real LFP in the gamma range. The bursts are non-overlapping, and the injected bursts are of duration 0.05 s, 0.075 s, and 0.1 to 1 s in steps of 0.1 s. The threshold fraction (see Section 2.3.5 for the definition) is set to 0.5. (B) Injected burst versus median burst lengths when the power of the injected burst matches that of the real LFP in the gamma range. Overlap of bursts is allowed, and the injected bursts are of duration 0.05 s, 0.075 s, and 0.1 to 1 s in steps of 0.1 s. The threshold fraction is set to 0.5.

Fig. 2.

(A) Convergence analysis of methods: Residue energy (percentage relative to the signal energy) versus iteration number. (B) Performance of atomic methods as a function of the dictionary size: Estimated burst durations for the three methods for various dictionary sizes when bursts of duration 300 ms are injected (shown as a dashed line with label Ref).

Fig. 3.

(A) Performance of atomic methods as a function of number of bursts injected: Normalized absolute error for increasing number of bursts when bursts of duration 300 ms are injected. (B) Performance of methods with varying threshold fractions: Mean number of bursts detected across 102 trials when the threshold fraction is varied between 0.06 and 0.9.

Fig. 4.

Visual illustration of the bursts detected by the different methods. Left: LFP overlaid with the detected atoms (LFP overlaid with the detected burst length for the Hilbert method); Right: Wigner–Ville time–frequency plots for atomic methods (power plot overlaid with detected burst length for the Hilbert method.)

Fig. 5.

Gamma duration estimation from real LFP data. (A) Median gamma duration for each electrode as a function of the change in the gamma power relative to spontaneous activity for monkey 1, for the four methods. (B) Histogram of the gamma durations from all sites for monkey 1. (C) Median gamma duration returned at each unique frequency by MP, OMP, OMP-MAGE, and OMP-GEAR, for monkey 1. (D) Median gamma duration per site as a function of the change in power relative to the mean gamma power from spontaneous activity at that site for monkey 2. (E) Histogram of gamma duration from all sites for monkey 2. (F) Median gamma duration returned at each unique frequency by MP, OMP, OMP-MAGE, and OMP-GEAR, for monkey 2. (G) Violin plots embedded with box plots of median burst lengths for all algorithms, for monkey 1. (H) Violin plots embedded with box plots of median burst lengths for all algorithms, for monkey 2.