Theoretical Modeling of a Bionic Arm with Elastomer Fiber as Artificial Muscle Controlled by Periodic Illumination
- PMID: 40808170
- PMCID: PMC12349628
- DOI: 10.3390/polym17152122
Theoretical Modeling of a Bionic Arm with Elastomer Fiber as Artificial Muscle Controlled by Periodic Illumination
Abstract
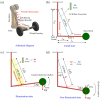
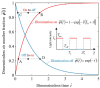
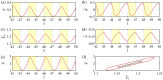
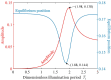
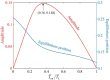
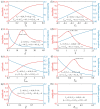
Liquid crystal elastomers (LCEs) have shown great potential in the field of soft robotics due to their unique actuation capabilities. Despite the growing number of experimental studies in the soft robotics field, theoretical research remains limited. In this paper, a dynamic model of a bionic arm using an LCE fiber as artificial muscle is established, which exhibits periodic oscillation controlled by periodic illumination. Based on the assumption of linear damping and angular momentum theorem, the dynamics equation of the model oscillation is derived. Then, based on the assumption of linear elasticity model, the periodic spring force of the fiber is given. Subsequently, the evolution equations for the cis number fraction within the fiber are developed, and consequently, the analytical solution for the light-excited strain is derived. Following that, the dynamics equation is numerically solved, and the mechanism of the controllable oscillation is elucidated. Numerical calculations show that the stable oscillation period of the bionic arm depends on the illumination period. When the illumination period aligns with the natural period of the bionic arm, the resonance is formed and the amplitude is the largest. Additionally, the effects of various parameters on forced oscillation are analyzed. The results of numerical studies on the bionic arm can provide theoretical support for the design of micro-machines, bionic devices, soft robots, biomedical devices, and energy harvesters.
Keywords: bionic arm; dynamic model; forced oscillation; light-fueled; liquid crystal elastomer; periodic illumination.
Conflict of interest statement
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Figures

Similar articles
-
Prescription of Controlled Substances: Benefits and Risks.2025 Jul 6. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2025 Jan–. 2025 Jul 6. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2025 Jan–. PMID: 30726003 Free Books & Documents.
-
Electrophoresis.2025 Jul 14. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2025 Jan–. 2025 Jul 14. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2025 Jan–. PMID: 36251838 Free Books & Documents.
-
Fast-Swimming Soft Robotic Fish Actuated by Bionic Muscle.Soft Robot. 2024 Oct;11(5):845-856. doi: 10.1089/soro.2023.0163. Epub 2024 Feb 26. Soft Robot. 2024. PMID: 38407844
-
Management of urinary stones by experts in stone disease (ESD 2025).Arch Ital Urol Androl. 2025 Jun 30;97(2):14085. doi: 10.4081/aiua.2025.14085. Epub 2025 Jun 30. Arch Ital Urol Androl. 2025. PMID: 40583613 Review.
-
Assessing the comparative effects of interventions in COPD: a tutorial on network meta-analysis for clinicians.Respir Res. 2024 Dec 21;25(1):438. doi: 10.1186/s12931-024-03056-x. Respir Res. 2024. PMID: 39709425 Free PMC article. Review.
References
-
- Sepehri S., Mashhadi M.M., Fakhrabadi M.S. Active/passive tuning of wave propagation in phononic microbeams via piezoelectric patches. Mech. Mater. 2022;167:104249. doi: 10.1016/j.mechmat.2022.104249. - DOI
LinkOut - more resources
Full Text Sources

