Linear and nonlinear multidimensional functional connectivity methods reveal similar networks for semantic processing in EEG/MEG data
- PMID: 40808809
- PMCID: PMC12343681
- DOI: 10.3389/fnhum.2025.1533034
Linear and nonlinear multidimensional functional connectivity methods reveal similar networks for semantic processing in EEG/MEG data
Abstract
Introduction: Investigating task- and stimulus-dependent connectivity is key to understanding how the interactions between brain regions underpin complex cognitive processes. Yet, the connections identified depend on the assumptions of the connectivity method. To date, methods designed for time-resolved electroencephalography/magnetoencephalography (EEG/MEG) data typically reduce signals in regions to one time course per region. This may fail to identify critical relationships between activation patterns across regions. Time-Lagged Multidimensional Pattern Connectivity (TL-MDPC) is a promising new EEG/MEG functional connectivity method improving previous approaches by assessing multidimensional relationships between patterns of brain activity. However, TL-MDPC remains linear and may therefore miss nonlinear interactions among brain areas.
Methods: Thus, we introduce Nonlinear TL-MDPC (nTL-MDPC), a novel bivariate functional connectivity method for event-related EEG/MEG applications, and compare its performance to the original linear TL-MDPC. nTL-MDPC describes how well patterns in ROI at a time point can predict patterns of ROI at a time point using artificial neural networks.
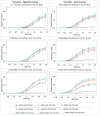
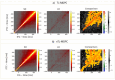
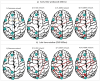
Results: Applying this method and its linear counterpart to simulated data demonstrates that both can identify nonlinear dependencies, with nTL-MDPC achieving up to ~0.75 explained variance under optimal conditions (e.g., high SNR), compared to ~0.65 with TL-MDPC. However, with a sufficient number of trials- e.g., a trials-to-vertex ratio ≥10:1 - nTL-MDPC achieves up to 15% higher explained variance than the linear method. Nevertheless, application to a real EEG/MEG dataset demonstrated only subtle increases in nonlinear connectivity strength at longer time lags with no significant differences between the two approaches.
Discussion: Overall, this suggests that linear multidimensional methods may be a reasonable practical choice to approximate brain connectivity, given the additional computational demands of nonlinear methods.
Keywords: EEG; MEG; event-related connectivity; functional connectivity; multidimensional; nonlinear; semantic control; semantic representation.
Copyright © 2025 Rahimi, Jackson and Hauk.
Conflict of interest statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Figures

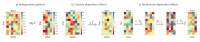



Similar articles
-
Prescription of Controlled Substances: Benefits and Risks.2025 Jul 6. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2025 Jan–. 2025 Jul 6. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2025 Jan–. PMID: 30726003 Free Books & Documents.
-
Time-Lagged Multidimensional Pattern Connectivity (TL-MDPC): An EEG/MEG pattern transformation based functional connectivity metric.Neuroimage. 2023 Apr 15;270:119958. doi: 10.1016/j.neuroimage.2023.119958. Epub 2023 Feb 21. Neuroimage. 2023. PMID: 36813063 Free PMC article.
-
Short-Term Memory Impairment.2024 Jun 8. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2025 Jan–. 2024 Jun 8. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2025 Jan–. PMID: 31424720 Free Books & Documents.
-
The Black Book of Psychotropic Dosing and Monitoring.Psychopharmacol Bull. 2024 Jul 8;54(3):8-59. Psychopharmacol Bull. 2024. PMID: 38993656 Free PMC article. Review.
-
Is functional brain connectivity atypical in autism? A systematic review of EEG and MEG studies.PLoS One. 2017 May 3;12(5):e0175870. doi: 10.1371/journal.pone.0175870. eCollection 2017. PLoS One. 2017. PMID: 28467487 Free PMC article.
References
-
- Anzellotti S., Fedorenko E., Kell A. J. E., Caramazza A., Saxe R. (2017b). Measuring and modeling nonlinear interactions between brain regions with fMRI. bioRxiv [Preprint]. bioRxiv: 74856
-
- Arinyo-i-Prats R., López-Madrona V. J., Paluš M. (2024). Lead/Lag directionality is not generally equivalent to causality in nonlinear systems: Comparison of phase slope index and conditional mutual information. NeuroImage. 292:120610., PMID: - PubMed
LinkOut - more resources
Full Text Sources

