Versatile photonic frequency synthetic dimensions using a single programmable on-chip device

Abstract

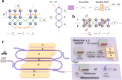
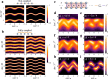
Investigating physical models with photonic synthetic dimensions has been generating great interest in vast fields of science. The rapidly developing thin-film lithium niobate (TFLN) platform, for its numerous advantages including high electro-optic coefficient and scalability, is well compatible with the realization of synthetic dimensions in the frequency together with spatial domain. While coupling resonators with fixed beam splitters is a common experimental approach, it often lacks tunability and limits coupling between adjacent lattices to sites occupying the same frequency domain positions. Here, on the contrary, we conceive the resonator arrays connected by electro-optic tunable Mach-Zehnder interferometers in our configuration instead of fixed beam splitters. By applying bias voltage and RF modulation on the interferometers, our design extends such coupling to long-range scenario and allows for continuous tuning on each coupling strength and synthetic effective magnetic flux. Therefore, our design enriches controllable coupling types that are essential for building programmable lattice networks and significantly increases versatility. As the example, we experimentally fabricate a two-resonator prototype on the TFLN platform, and on this single chip we realize well-known models including tight-binding lattices, the Hall ladder and Creutz ladder. We directly observe the band structures in the quasi-momentum space and important phenomena such as spin-momentum locking, flat band and the Aharonov-Bohm cage effect. These results demonstrate the potential for convenient simulations of more complex models in our configuration.

Fig. 1. Schematic and experimental setup.

a Configuration of a lattice network in frequency synthetic dimensions. The lattice network is simulated by a train of modulated resonators. Instead of fixed beam splitters (BS), MZIs tunable by DC and RF signals are used to couple the adjacent resonators (purple boxes). The lattice network consequently contains three types of coupling $J_{i,p}^H$ (orange), $J_i^V$ (violet), $J_{i,p}^C$ (green), where i is the index of resonators (A_i) along the spatial direction, and p is the coupling range along the frequency direction. These couplings stem from RF signals on the resonators, DC and RF signals applied on the MZIs, respectively. ${\varphi }_{i,p}^H$, ${\varphi }_i^V$, ${\varphi }_{i,p}^C$ are the corresponding phases accumulated while coupling, which stem from the initial phases of the modulation. b Schematic of the Creutz ladder consisting of two lattices A and B which serve as two pseudospins. The coupling types are of same definition in a and are abbreviated as $J_{A\left(B\right)}^H$, J^V and J^C. The phases accumulated around the rectangular or triangular plaquettes form gauge potentials such as ϕ₁, ϕ₂ and ϕ₃. c Experimental setup for realizing b with two MZI assisted race-track resonators on TFLN. Three sets of electrical signals consisting of DC and RF parts are applied on three sets of the ground-signal-ground (GSG) arranged electrodes through Bias-Tees to control the two resonators (S₁, S₃) and the MZI (S₂). For detecting band structures, a probe laser with detuning Δω is injected to excite the bands. The time- (quasi-momentum-) varying transmittance signal, which is a slice of the band structure, is detected by a photodetector (PD) followed by an oscilloscope triggered by the RF source. For obtaining mode distribution, the measurement part is replaced by scanning a Fabry–Perot (F-P) cavity together with a photodetector.

Fig. 2. Experimental obtained band structures of tight-binding lattices and the Hall ladder.

The band structures exhibit tight-binding lattice characters when two resonators are either not coupled (J^V = 0, a) or fully coupled into a large resonator whose length is doubled and FSR is halved (b). $J_B^H$ is set to zero in the left panels of (b), while set to be equal to $J_A^H$ in the right panels. The right panel in (a) and the lower panels in (b) are the corresponding numerical calculations. c Illustration of the Hall ladder where the crossing coupling is absent. d–g The heat maps are the experimentally obtained band structures of the Hall ladder with coupling strength ratio $r_{VH}=J_V/2J_H=0.75$, J^H = 0.06Ω and an effective magnetic flux ϕ₁ being  ± π/4 or  ± 3π/4. h, i are the numerical calculations of (f and g). The population information on the two spins (resonators) are encoded in the normalized intensities. Choosing the opposite flux (ϕ₁) is equivalent to selectively exciting the opposite spin. For one spin (d and e), the negative (positive) k states in the first Brillouin zone predominate the upper (lower) bands. Meanwhile, complementary patterns appear in the other spin (f and g), signifying the spin-momentum locking.

Fig. 3. Experimental obtained band structures of the Creutz ladder and direct observation of the Aharonov–Bohm cage effect.

a Illustration of the Creutz ladder. b, c The heat maps display two general band structures of the Creutz ladder given different ϕ₁ and ϕ^C, where J^V/2J^H = 1.1, J^C/J^H = 0.52 and J^H = 0.06Ω. d The flat band structure measured at J^V = 0, J^H = J^C = 0.028Ω and $-{\varphi }_A^H={\varphi }_B^H=\pi /2$. The absence of J^V, equal J^H and J^C, together with the π flux also satisfy the Aharonov–Bohm cage effect condition. The left panels in (b–d) are the experimental results and the right panels are the numerical calculations. The population information on the two spins (resonators) are encoded in the normalized intensities. e Illustration of the Aharonov–Bohm cage effect where the phase collected in a round trip in the pink area is π. When a probe light is input from resonator A with frequency near the zero index mode, the distribution is caged within the dashed box (0, ±1 in lattice A and  ±1 in lattice B). f, g The blue points are the experimental readout of the mode distribution from the drop ports of resonator A and B measured by a Fabry–Perot (F-P) cavity. The pink dashed lines represent the normalized numerical calculations, where Δω is fitted to be approximate 4J^H. The distribution other than those inside the dashed box is clearly suppressed. h Illustration of the not caged situation where the phase collected in the pink area is zero. The light normally spreads out along the frequency direction. i, j The blue points are experimental results of the not caged situation, where more modes survives compared to the caged ones. The pink circles and dashed lines represent the normalized numerical calculations, where Δω is fitted to be approximate 2J^H. The distribution results are plotted in the logarithmic coordinates and the linewidth of the F-P cavity is taken into account.