Annotation-free discovery of disease-relevant cells in single-cell datasets
- PMID: 40864714
- PMCID: PMC12383263
- DOI: 10.1126/sciadv.adv5019
Annotation-free discovery of disease-relevant cells in single-cell datasets
Abstract
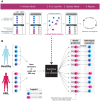
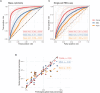
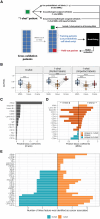
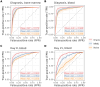
In single-cell datasets, patient labels indicating disease status (e.g., "sick" or "not sick") are typically available, but individual cell labels indicating which of a patient's cells are associated with their disease state are generally unknown. To address this, we introduce mixture modeling for multiple-instance learning (MMIL), an expectation-maximization approach that trains cell-level binary classifiers using only patient-level labels. Applied to primary samples from patients with acute leukemia, MMIL accurately separates leukemia from nonleukemia baseline cells, including rare minimal residual disease (MRD) cells; generalizes across tissues and treatment time points; and identifies biologically relevant features with accuracy approaching that of a hematopathologist. MMIL can also incorporate cell labels when they are available, creating a robust framework for leveraging both labeled and unlabeled cells. MMIL provides a flexible modeling framework for cell classification, especially in scenarios with unknown gold-standard cell labels.
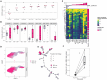
Figures



References
-
- Gulati G. S., D’Silva J. P., Liu Y., Wang L., Newman A. M., Profiling cell identity and tissue architecture with single-cell and spatial transcriptomics. Nat. Rev. Mol. Cell Biol. 26, 11–31 (2025). - PubMed
-
- Hanahan D., Hallmarks of cancer: New dimensions. Cancer Discov. 12, 31–46 (2022). - PubMed
-
- Spitzer M. H., Gherardini P. F., Fragiadakis G. K., Bhattacharya N., Yuan R. T., Hotson A. N., Finck R., Carmi Y., Zunder E. R., Fantl W. J., Bendall S. C., Engleman E. G., Nolan G. P., IMMUNOLOGY., An interactive reference framework for modeling a dynamic immune system. Science 349, 1259425 (2015). - PMC - PubMed
-
- Lo Y. C., Liu Y., Kammersgaard M., Koladiya A., Keyes T. J., Davis K. L., Single-cell technologies uncover intra-tumor heterogeneity in childhood cancers. Semin. Immunopathol. 45, 61–69 (2023). - PubMed
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

