Including the Magnitude Variability of a Signal in the Ordinal Pattern Analysis

Abstract

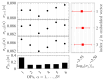
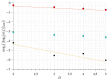
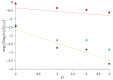
One of the most popular and innovative methods to analyse signals is by using Ordinal Patterns (OPs). The OP encoding is based on transforming a (univariate) signal into a symbolic sequence of OPs, where each OP represents the number of permutations needed to order a small subset of the signal's magnitudes. This implies that OPs are conceptually clear, methodologically simple to implement, and robust to noise, and that they can be applied to short signals. Moreover, they simplify the statistical analyses that can be carried out on a signal, such as entropy and complexity quantifications. However, because of the relative ordering, information about the magnitude of the signal at each timestamp is lost-this being one of the major drawbacks of this method. Here, we propose a way to use the signal magnitudes discarded in the OP encoding as a complementary variable to its permutation entropy. To illustrate our approach, we analyse synthetic trajectories from logistic and Hénon maps-with and without added noise-and real-world signals, including intracranial electroencephalographic recordings from rats in different sleep-wake states and frequency fluctuations in power grids. Our results show that, when complementing the permutation entropy with the variability in the signal magnitudes, the characterisation of these signals is improved and the results remain explainable. This implies that our approach can be useful for feature engineering and improving AI classifiers, as typical machine learning algorithms need complementary signal features as inputs to improve classification accuracy.

Keywords: feature extraction; ordinal patterns; permutation entropy; signal analysis.

Figure A1

Rényi min-entropy and average magnitude variability of the ordinal pattern (OP) embedded vectors from two coupled identical logistic maps. The map iterates for the OP encoding are obtained from Equation (1), where the coupling strength $\epsilon$ is set to $0.01$ or $0.2$ and the map parameter r is set to $3.6$ (red symbols), $3.75$ (black symbols), $3.8$ (cyan symbols), or $3.9$ (yellow symbols). We use $D=4$ and $\tau =1$ for the OP encoding of the iterates of the y component (one map)—see Section 2 for details.

Figure A2

Rényi min-entropy and average magnitude variability of the ordinal pattern (OP) embedded vectors from a Hénon map. The map iterates are obtained from Equation (2) with $b=0.3$ and the other parameter set to either $a=1.15$ (red circle), $1.20$ (black square), $1.34$ (cyan diamond), $1.35$ (yellow triangle), $1.40$ (black asterisk), or $1.405$ (green triangle). We use $D=4$ and $\tau =1$ for the OP encoding of the iterates of the y component (as in Figure A1)—see Section 2 for details.

Figure 1

Example of the variability of EEG signal magnitudes within each ordinal pattern (OP). The EEG signal is from the right primary motor cortex (rM1) of a representative rat during active wakefulness and the OPs are constructed using an embedding dimension $D=3$ and delay $\tau =1$. The top three left panels show the values of the standard deviation of the EEG signal ${\sigma }_j\left(\alpha \right)$ in the components ($j=1,2,3$) of the embedded vectors for each OP symbol ($\alpha =1,\dots ,6$). The bottom left panel shows the OP probability distribution ${\left\{P\left(\alpha \right)\right\}}_{\alpha =1}^{D!}=\{P\left(1\right),\dots ,P(D!=6)\}$. The right panel shows the mean (red squares) with respect to ${\left\{P\left(\alpha \right)\right\}}_{\alpha =1}^6$ for each set of ${log}_2\left[{\sigma }_j\left(\alpha \right)\right]$ values, $\langle {log}_2\left[{\sigma }_j\right]\rangle$, with error bars defined by $\pm \sqrt{\langle {log}_2{\left[{\sigma }_j\right]}^2\rangle -{\langle {log}_2\left[{\sigma }_j\right]\rangle }^2}$.

Figure 2

Rényi min-entropy and average magnitude variability of the ordinal pattern (OP) embedded vectors from two coupled identical logistic maps. The map iterates for the OP encoding are obtained from Equation (1), where the coupling strength $\epsilon$ is set to $0.01$ or $0.2$ and the map parameter r is set to $3.6$ (red symbols), $3.75$ (black symbols), $3.8$ (cyan symbols), or $3.9$ (yellow symbols). We use $D=4$ and $\tau =1$ for the OP encoding of the iterates of the x component (one map)—see Section 2 for details.

Figure 3

Bifurcation-like diagrams for coupled identical logistic maps. The left [right] panel shows the signal of one map, $x_t$ (Equation (1)), when $\epsilon =0.01$ [$\epsilon =0.2$] as r is changed according to the values used in Figure 2.

Figure 4

Rényi min-entropy and average magnitude variability of the ordinal pattern (OP) embedded vectors from a Hénon map. The map iterates are obtained from Equation (2) with $b=0.3$ and the other parameter set to either $a=1.15$ (red circle), $1.20$ (black square), $1.34$ (cyan diamond), $1.35$ (yellow triangle), $1.40$ (black asterisk), or $1.405$ (green triangle). We use $D=4$ and $\tau =1$ for the OP encoding of the iterates of the x component (as in Figure 2)—see Section 2 for details.

Figure 5

Average magnitude variability of the ordinal pattern sequences from two coupled identical logistic maps as a function of the embedding dimension D and noise strength. Black squares correspond to noiseless iterates, cyan diamonds to observational noise with a standard deviation of ${10}^{-1}$, and red circles to observational noise with a standard deviation of ${10}^0$. The map parameters for all symbols are set such that $r=3.6$ and $\epsilon =0.01$ (Equation (1)). Two reference lines are included with slopes of $-2$ (orange) and $-1/2$ (red).

Figure 6

Average magnitude variability of the ordinal pattern (OP) sequences from a Hénon map as a function of the OP embedding dimension and noise strength. Filled symbols have the same observational noise as in Figure 5. The map parameters of the Hénon map are $b=0.3$ and $a=1.15$ (Equation (2)). Two reference lines are included with slopes of $-2$ (orange) and $-1/2$ (red).

Figure 7

OPs analysis for EEG recordings from 11 rats in three sleep–wake states: active wakefulness (AW), rapid eye movement (REM) and non-REM (NREM) sleep. (A) Location of the electrodes for the EEG recordings corresponding to the right olfactory bulb (OB), and the primary motor (M1) and somatosensory (S1) cortices. (B–D) Rényi entropy vs. average magnitude variability, respectively, for BO, M1, and S1 electrodes. The embedding dimension for the OPs is $D=5$.

Figure 8

OPs analysis for GPS-synchronised grid frequency recording from 4 different locations in the European synchronous electric power grid: Karlsruhe (KA), Oldenburg (OL), Lisbon (PT), Istanbul (TU). Rényi min-entropy vs. average magnitude variability for the different locations and five different 24 h periods of recordings (respectively corresponding to the five different symbols). The embedding dimension for the OPs is $D=5$.