Microrheology: From Video Microscopy to Optical Tweezers
- PMID: 40872425
- PMCID: PMC12388072
- DOI: 10.3390/mi16080918
Microrheology: From Video Microscopy to Optical Tweezers
Abstract
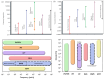
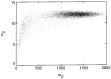
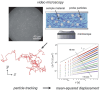
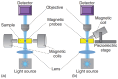
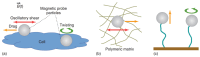
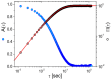
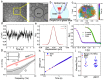
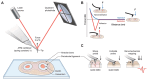
Microrheology, a branch of rheology, focuses on studying the flow and deformation of matter at micron length scales, enabling the characterization of materials using minute sample volumes. This review article explores the principles and advancements of microrheology, covering a range of techniques that infer the viscoelastic properties of soft materials from the motion of embedded tracer particles. Special emphasis is placed on methods employing optical tweezers, which have emerged as a powerful tool in both passive and active microrheology thanks to their exceptional force sensitivity and spatiotemporal resolution. The review also highlights complementary techniques such as video particle tracking, magnetic tweezers, dynamic light scattering, and atomic force microscopy. Applications across biology, materials science, and soft matter research are discussed, emphasizing the growing relevance of particle tracking microrheology and optical tweezers in probing microscale mechanics.
Keywords: atomic force microscopy; diffusing wave spectroscopy; dynamic light scattering; magnetic tweezers; microrheology; optical tweezers; rheology; video particle tracking.
Conflict of interest statement
The authors declare no conflicts of interest.
Figures











Similar articles
-
Prescription of Controlled Substances: Benefits and Risks.2025 Jul 6. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2025 Jan–. 2025 Jul 6. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2025 Jan–. PMID: 30726003 Free Books & Documents.
-
PyFMLab: Open-source software for atomic force microscopy microrheology data analysis.Open Res Eur. 2024 Jul 24;3:187. doi: 10.12688/openreseurope.16550.2. eCollection 2023. Open Res Eur. 2024. PMID: 39118808 Free PMC article.
-
Information-Providing Magnetic Supraparticles: Particle Designs to Record Environmental Stimuli with Readout by Magnetic Particle Spectroscopy.Acc Mater Res. 2025 May 23;6(7):842-852. doi: 10.1021/accountsmr.5c00027. eCollection 2025 Jul 25. Acc Mater Res. 2025. PMID: 40741230
-
Magnetic resonance perfusion for differentiating low-grade from high-grade gliomas at first presentation.Cochrane Database Syst Rev. 2018 Jan 22;1(1):CD011551. doi: 10.1002/14651858.CD011551.pub2. Cochrane Database Syst Rev. 2018. PMID: 29357120 Free PMC article.
-
Management of urinary stones by experts in stone disease (ESD 2025).Arch Ital Urol Androl. 2025 Jun 30;97(2):14085. doi: 10.4081/aiua.2025.14085. Epub 2025 Jun 30. Arch Ital Urol Androl. 2025. PMID: 40583613 Review.
References
-
- Einstein A. In: Investigations on the Theory of the Brownian Movement. Fürth R., editor. Dover Publications, Inc.; New York, NY, USA: 1956.
-
- Perrin J. Atoms. Constable; London, UK: 1916.
-
- Tassieri M. Microrheology with Optical Tweezers: Peaks & Troughs. Curr. Opin. Colloid Interface Sci. 2019;43:39–51. doi: 10.1016/j.cocis.2019.02.006. - DOI
Publication types
LinkOut - more resources
Full Text Sources

