randPedPCA: rapid approximation of principal components from large pedigrees

Abstract

Background: Pedigrees continue to be extremely important in agriculture and conservation genetics, with the pedigrees of modern breeding programmes easily comprising millions of records. This size can make visualising the structure of such pedigrees challenging. Being graphs, pedigrees can be represented as matrices, including, most commonly, the additive (numerator) relationship matrix, $A$ , and its inverse. With these matrices, the structure of pedigrees can then, in principle, be visualised via principal component analysis (PCA). However, the naive PCA of matrices for large pedigrees is challenging due to computational and memory constraints. Furthermore, computing a few leading principal components is usually sufficient for visualising the structure of a pedigree.

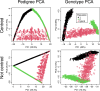
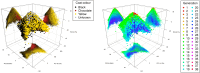
Results: We present the open-access R package randPedPCA for rapid pedigree PCA using sparse matrices. Our rapid pedigree PCA builds on the fact that matrix-vector multiplications with the additive relationship matrix can be carried out implicitly using the extremely sparse inverse relationship factor, $L^{-1}$ , which can be directly obtained from a given pedigree. We implemented two methods. Randomised singular value decomposition tends to be faster when very few principal components are requested, and Eigen decomposition via the RSpectra library tends to be faster when more principal components are of interest. On simulated data, our package delivers a speed-up greater than 10,000 times compared to naive PCA. It further enables analyses that are impossible with naive PCA. When only two principal components are desired, the randomised PCA method can half the running time required compared to RSpectra, which we demonstrate by analysing the pedigree of the UK Kennel Club registered Labrador Retriever population of almost 1.5 million individuals.

Conclusions: The leading principal components of pedigree matrices can be efficiently obtained using randomised singular value decomposition and other methods. Scatter plots of these scores allow for intuitive visualisation of large pedigrees. For large pedigrees, this is considerably faster than rendering plots of a pedigree graph.

Algorithm 1

Efficiently multiplying the additive relationship matrix $\mathit{A}$ with a vector $\mathit{x}$ via the Cholesky factor, ${\mathit{L}}^{-1}$, of the precision matrix

Algorithm 2

Efficiently multiplying the ‘centred’ additive relationship matrix $\tilde{\mathit{A}}$ with a vector $\mathit{x}$ via the Cholesky factor, ${\mathit{L}}^{-1}$, of the precision matrix

Algorithm 3

Approximate PCA of the additive relationship matrix $\mathit{A}$ (possibly ‘centred’) via the randomised SVD of the precision matrix’s Cholesky factor ${\mathit{L}}^{-1}$

Fig. 1

Scatter plots of the first two principal components computed from the pedigree and SNP genotypes of the 2pop scenario with centring (top row) or without centring (bottom row). The plots on the left were generated with randPedPCA and thus show approximate scores and percentage of captured variance. We ran the standard PCA on all SNP markers. The legend applies to all panels.

Fig. 2

Scatter plots of the first two principal components computed from the pedigree and SNP genotypes of the 4pop scenario with centring (top row) or without centring (bottom row). The plots on the left were generated with randPedPCA and thus show approximate scores and percentage of captured variance. We ran the standard PCA on all genotype markers. The legend applies to all panels

Fig. 3

3D scatter plots of the first three principle components for the UK Kennel Club’s Labrador Pedigree from 1955 to 2024. The left-hand plot highlights coat colour, while the right-hand plot highlights generation. Projections onto coordinate planes are provided with the same colour used in the main plots.