Robust bilinear rotations

Abstract

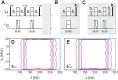
Bilinear rotation elements allow interaction-dependent manipulations of spins in quantum technologies and, particularly, in spectroscopy. We used bilinear rotation in nuclear magnetic resonance (NMR) spectroscopy and derived several ways of introducing robustness into the filter element. We distinguished two performance levels: the coupling dependent inversion of polarization and the full bilinear π-rotation capability. In addition, all four essential variants of bilinear π rotations-BIRD^d, BIRD^r, BIRD^d,X, and BIRD^r,X filters-were given for all cases studied. In the first step, adiabatic CHIRP-type and BUBI/BUBU pulses lead to improved robustness with respect to offset/detuning effects and variations in B₁-field strengths. In the second step, we optimized time-optimal coupling-compensated BIRD elements. Together with correspondingly optimized pulse shapes, we established fully coupling, offset, and B₁-compensated bilinear π-rotation (COB-BIRD) elements and characterized them in theory and experiment. Overall, this demonstrated the use of the robust bilinear rotation capability on a partially aligned sample in a homodecoupled two-dimensional NMR experiment.

Fig. 1.. Theoretical comparison of the BIRD and JC-BIRD pulse sequences on their efficacy of spin inversion and universal rotation to a variation in J coupling.

Original BIRD (A) and JC-BIRD (B) pulse sequences (4, 5) and their robustness against J coupling variations (C and D). Solid and open rectangles correspond to 90° and 180° pulses, respectively; phases are x unless indicated otherwise, and transfer delays are calibrated to match Δ = 1/(2 × ¹J_CH). The phases ϕ₁ to ϕ₄ of the BIRD sequence (A) can be manipulated according to Table 1 to obtain the four possible effective bilinear rotations. If ϕ₄ is not indicated, the dashed pulse is left out. The ${\mathrm{\Phi }}_{\text{PP}}$ (C) and ${\mathrm{\Phi }}_{\text{UR}}^{*}$ (D) fidelities of both the BIRD^d,X element (solid blue, ϕ₃ = x, no dashed 180° pulse applied) and the JC-BIRD^d,X element (dashed orange) are simulated using on-resonant hard pulses and Δ = 1/(2 × 185 Hz).

Fig. 2.. The use of offset-compensated adiabatic or optimal control–derived pulses in the BIRD and JC-BIRD to extend the robustness into offset variation.

(A) Alternative pulse sequence for BIRD elements based on a pair of adiabatic pulses to achieve offset-compensated optimal transfer of the BIRD^d bilinear rotation. Trapezoids correspond to adiabatic pulses with their sweep direction indicated by the arrows. Universal rotation refocusing (UR-180°) and point-to-point inversion pulses [PP(z-z)] are presented as open rectangles with a dash or a curved diagonal, respectively. (B) A JC-BIRD sequence using a pair of BUBI and a single BUBU pulse sandwich for offset compensation is shown. Transfer delays are calibrated to match Δ = 1/(2 × ¹J_CH). (C, E, G, and I) The simulations of ${\mathrm{\Phi }}_{\text{PP}}$ (left column) and (D, F, H, and J) ${\mathrm{\Phi }}_{\text{UR}}^{*}$ (right column) of the BIRD elements with respect to the offset frequency v_S and J coupling for hard-pulse BIRD^d [(C) and (D)] and JC-BIRD^d [(E) and (F)], as well as the offset-compensated adiabatic BIRD^d [(G) and (H)] and BUBI/BUBU-JC-BIRD^d [(J) and (K)]. Hard pulses were simulated with an rf amplitude of 25 kHz, corresponding to a 10-μs 90° pulse. Adiabatic WURST₄₀ pulses with T = 1 ms, Q = 5, and a sweep-width Δv_S = 40 kHz and BUBI/BUBU pulse sandwiches as specified in Table 2 were used in the simulations. Contour levels in all cases equal 0.8 (indigo), 0.9 (orange), 0.94 (ultramarine), and 0.97 (magenta).

Fig. 3.. TOP performance curves for optimal control–derived JC-BIRD elements.

Continuous shapes as well as hard-pulse delay sequences with, neglecting 180° pulses in refocused delays, (n + 1) proton pulses and (n) delays were evaluated using ${\mathrm{\Phi }}_{\text{UR}}$ and taking only the on-resonance performance with respect to J into account. Different TOP curves are represented with different colors as specified on the top of the graph. While the shape TOP curve marks roughly the physical limit for the bilinear rotation, hard-pulse delay sequences are needed for actual robust implementations. The performances of the original BIRD (2p1d due to the two 90° pulses flanking the refocused delay) and JC-BIRD (4p3d) sequences as well as the 4p3d sequence used subsequently for the COB-BIRD implementation are annotated correspondingly.

Fig. 4.. Comparison of experimental and simulated data to the universal π rotation of the BIRD^d and the COB-BIRD^d.

Experimental demonstration (black spectral series) of the BIRD^d (A) and the COB-BIRD^d (B) sequences, as well as their comparison to corresponding simulations (superimposed red lines). Experimental data were obtained as described in the main text, and simulations show ${\mathrm{\Phi }}_{\text{PP}}(I_x\to I^{-})$ fidelities on the highlighted elements using on-resonant hard pulses. The COB-BIRD^d pulse sequence is given in Fig. 5.

Fig. 5.. The four essential COB-BIRD pulse sequences and their experimental fidelities for spin inversion and universal π rotation against coupling and offset variation.

(A) The general sequence for the COB-BIRD. For effective bilinear π rotations in the coupling range of 120 to 250 Hz, all delays δ₁ = 2.583 ms. Universal rotation refocusing (UR-180°) and point-to-point inversion pulses [PP(z-z)] of pulse sandwiches are applied as indicated. By replacing the gray box with either (B) or (C) and setting the flip angle ϕ₅ accordingly, all four different COB-BIRD bilinear rotations can be implemented. In order to design the COB-BIRD^r,X or the COB-BIRD^d,X, fragment (B) is used with ϕ₅ set to −148° or 32°, respectively, and in order to design the COB-BIRD^d or COB-BIRD^r, fragment (C) is used with ϕ₅ set to −148° or 32°, respectively. As an example, the ${\mathrm{\Phi }}_{\text{PP}}$ (D) and ${\mathrm{\Phi }}_{\text{UR}}^{*}$ (E) fidelities for the COB-BIRD^r,X variant are simulated with respect to v_S and J. Contours are scaled the same way as in Fig. 2.

Fig. 6.. Experimental comparison of various refocusing elements applied in a ¹³C-detected, ¹H-decoupled, and refocused J-INEPT experiment.

(A) The corresponding sequence with a gray box for different inversion elements and a COB3-INEPT transfer step is shown together with the structure and aromatic numbering of nicotine on top of the spectra. All pulses are applied along x unless indicated otherwise, and solid and open bars refer to 90° and 180° pulses, respectively, unless a different flip angle (136°) is annotated. For the refocusing elements, a simple 180° hard-pulse spin echo (B) is compared to the BIRD^d,X (C), the JC-BIRD^d,X (D), and the COB-BIRD^d,X (E) elements. All four 2D spectra were applied to a partially aligned sample of (−)-nicotine as explained in the main text. For each experiment, slices of the aromatic signals are extracted over the F1 dimension and shown with the corresponding measured T coupling and signal-to-noise-ratio (S/N). The transfer delays in the BIRD^d,X and JC-BIRD^d,X are set to 125 Hz to accommodate the small couplings, and the COB-BIRD^d,X is applied as presented in Fig. 5. Gradients of 1-ms duration and 200-μs recovery delay are applied in percent of the maximum gradient strength of nominally 53.5 G/cm according to G₁ = 7%, G₂ = 25%, G₃ = −G₄ = 10%, G₅ = 60%, and G₆ = 80%. Delays are δ_g = 1.2 ms, δ₂ = 0.5401 ms, δ₃ = 1.065 ms, and δ₄ = 1.0702 ms. For a detailed description including phase cycling and the particular 180° element used, refer to the Supplementary Materials (fig. S14).