Lie symmetry approach to the dynamical behavior and conservation laws of actin filament electrical models
- PMID: 40924812
- PMCID: PMC12419668
- DOI: 10.1371/journal.pone.0331243
Lie symmetry approach to the dynamical behavior and conservation laws of actin filament electrical models
Abstract
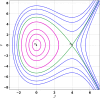
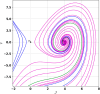
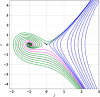
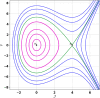
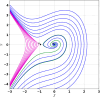
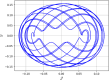
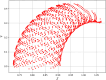
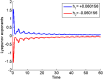
This research explores the dynamical properties and solutions of actin filaments, which serve as electrical conduits for ion transport along their lengths. Utilizing the Lie symmetry approach, we identify symmetry reductions that simplify the governing equation by lowering its dimensionality. This process leads to the formulation of a second-order differential equation, which, upon applying a Galilean transformation, is further converted into a system of first-order differential equations. Additionally, we investigate the bifurcation structure and sensitivity of the proposed dynamical system. When subjected to an external force, the system exhibits quasi-periodic behavior, which is detected using chaos analysis tools. Sensitivity analysis is also performed on the unperturbed system under varying initial conditions. Moreover, we establish the conservation laws associated with the equation and conduct a stability analysis of the model. Employing the tanh method, we derive exact solutions and visualize them through 3D and 2D graphical representations to gain deeper insights. These findings offer new perspectives on the studied equation and significantly contribute to the understanding of nonlinear wave dynamics.
Copyright: © 2025 Beenish et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures






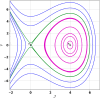
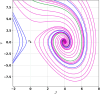
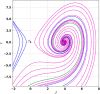














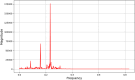

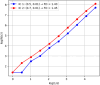

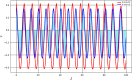

References
-
- Li L, Cheng B, Dai Z. Novel evolutionary behaviors of N-soliton solutions for the (3 1)-dimensional generalized Camassa–Holm–Kadomtsev–Petciashvili equation. Nonlinear Dynamics. 2024;112(3):2157–73.
-
- Liu HD, Tian B, Feng SP, Chen YQ, Zhou TY. Integrability, bilinearization, Bäcklund transformations and solutions for a generalized variable-coefficient Gardner equation with an external-force term in a fluid or plasma. Nonlinear Dynamics. 2024;112(14):12345–59.
-
- Yang H, Zhang X, Hong Y. Classification, production and carbon stock of harvested wood products in China from 1961 to 2012. BioResources. 2014;9(3):4311–22.
MeSH terms
LinkOut - more resources
Full Text Sources

