Entangled measurement for W states

Abstract

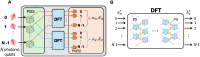
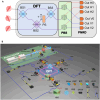
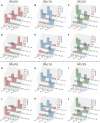
Entangled measurements are an indispensable tool for quantum information processing, such as Bell-state measurements in quantum teleportation and entanglement swapping. However, to date, the realization of entangled measurements has mainly focused on bipartite systems or Greenberger-Horne-Zeilinger (GHZ) states. Here, we demonstrate a practical scheme to realize entangled measurements for [Formula: see text] states. Thanks to the cyclic shift symmetry in the discrete Fourier transformation (DFT) of bosonic modes, the DFT measurement outcomes can be used to deterministically project multiqubit states onto [Formula: see text] states. Experimentally, we show that three-qubit [Formula: see text] state discrimination can be achieved by detecting the cyclic shift symmetry with a three-mode DFT optical circuit, yielding a measurement discrimination fidelity of 0.871 ± 0.039. Our experimental demonstration opens the door for the development of new quantum network protocols between multipartite systems.

Fig. 1.. W state measurement using CSS.

(A) Schematic diagram of entangled measurement for $W$ state in the photonic qubits encoded by polarization. PBS, polarizing beam splitter; DFT, discrete Fourier transformation; PNRD, photon number resolving detector. (B) Schematic diagram of $N$-mode DFT linear optical circuit: BS, beam splitter; PS, phase shifter.

Fig. 2.. Experimental setup.

(A) Schematic setup for three-qubit entangled measurement for a $W$ state. (B) Experimental setup for the evaluation of a $W$ state entangled measurement. BBO, beta-barium borate; BPF, band-pass filter (780 ± 1 nm); SPCM, single photon counting module; HBS, hybrid BS; LCVR, liquid crystal variable retarder; FPBS, fiber PBS; PMF, polarization-maintaining fiber; SHG, second harmonic generation.

Fig. 3.. Experimental results for K value correlation tables.

(A) to (C) show the ideal detection-probability distributions for $\mid W_3(0)\rangle$ , $\mid W_3(1)\rangle$ , and $\mid W_3(2)\rangle$ , respectively. (D) to (F) show the experimentally obtained detection-probability distributions for $\mid W_3(0)\rangle$ , $\mid W_3(1)\rangle$ , and $\mid W_3(2)\rangle$ , respectively. (G) to (I) show the ideal detection-probability distributions for $\mid {\overline{W}}_3(0)\rangle$ , $\mid {\overline{W}}_3(1)\rangle$ , and $\mid {\overline{W}}_3(2)\rangle$ , respectively. (J) to (L) show the experimentally obtained detection-probability distributions for $\mid {\overline{W}}_3(0)\rangle$ , $\mid {\overline{W}}_3(1)\rangle$ , and $\mid {\overline{W}}_3(2)\rangle$ , respectively. The total $K$ value is obtained as $K=K_{\mathrm{H}}+K_{\mathrm{V}}\left(\text{mod}3\right)$ . The red, blue, and green bars indicate the total $K$ values of zero, one, and two, respectively.

Fig. 4.. Sum of probabilities for identical K values.

(A) and (B) correspond to $W$ state components $\mid W_3(K)\rangle$ and $\mid {\overline{W}}_3(K)\rangle$ , respectively. For the input state $\mid {\mathrm{\psi }}_0\rangle$ , the MDFs of $\mid W_3(0)\rangle$ and $\mid {\overline{W}}_3(0)\rangle$ are obtained as 0.882 ± 0.038 and 0.884 ± 0.038. For the $\mid {\mathrm{\psi }}_1\rangle$ , the MDFs of $\mid W_3(1)\rangle$ and $\mid {\overline{W}}_3(2)\rangle$ are 0.870 ± 0.040 and 0.865 ± 0.038. For $\mid {\mathrm{\psi }}_1\rangle$ , the MDFs of $\mid W_3(2)\rangle$ and $\mid {\overline{W}}_3(1)\rangle$ are 0.862 ± 0.040 and 0.861 ± 0.039.

Fig. 5.. Schematic diagram of three-mode discrete DFT optical circuit.

(A) Original method to construct DFT. (B) Sagnac architecture DFT.

Fig. 6.. Schematic setup for photon sources.