On-chip multi-timescale spatiotemporal optical synchronization

Abstract

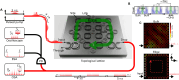
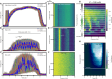
Mode locking is foundational to nonlinear optics, enabling advances in metrology, spectroscopy, and communications. However, it remains unexplored in nonharmonic, multi-timescale regimes. Here, we realize on-chip multi-timescale synchronization using topological photonics. We design a two-dimensional lattice of 261 coupled silicon nitride ring resonators that supports nested mode-locked states with fast ( [Formula: see text] 1 terahertz) single-ring and slow ( [Formula: see text] 3 gigahertz) topological super-ring timescales. We observe clear signatures of multi-timescale mode locking, including a quadratic distribution of pump noise across both azimuthal mode families, consistent with theory. These findings are supported by near-transform-limited repetition beats and the emergence of periodic temporal patterns on the slow timescale. The edge-confined states show distinct dynamics from bulk and single-ring modes, enabling clear identification. Our results establish topological frequency combs as a robust platform for independently tunable, lattice-scale synchronization, opening new directions for exploring the interplay of nonlinearity and topology in integrated photonics.

Fig. 1.. Concept of topological multi-timescale mode locking.

(A) Schematic of the experimental setup for the generation and detection of topological temporal mode-locked states in a simplified 2D array of coupled Kerr-ring resonators (see fig. S1 for the actual device). A tunable pulsed pump with a 5-ns pulse duration and 4-$\mathrm{\mu }$ s repetition period is coupled into the lattice at the input port and circulates around the edge of the 2D AQH SiN lattice (here, only the clockwise mode is shown). The generated frequency combs are directly analyzed using an OSA, revealing the comb spacing of the single rings ${\mathrm{\nu }}_{\mathrm{F}}$ and the nested comb spacing of the super-ring ${\mathrm{\nu }}_{\mathrm{S}}$ . The frequency combs are also recorded with a PD and analyzed with an oscilloscope and ESA, revealing the repetition rate of the combs and their time-domain dynamics. (B) Simulated linear transmission of the device. The edge and bulk bands of the spectrum are shaded in green and gray, respectively. (C) Simulated spatial profile of representative edge (bottom) and (top) bulk modes in the linear regime (shown only for the clockwise excitation.)

Fig. 2.. Optical spectrum analysis.

(A) Broadband optical spectrum of topological combs versus pump wavelength at an average pump power of $\sim$185 mW. Bulk and edge regions are shaded in gray and green, respectively. Three representative snapshots are shown on the right. (B) (Left) Measured spatial intensity profiles of bulk and edge combs; (right) corresponding linear simulations with only clockwise excitation. The device is the same design as in (A) but exhibits higher local scattering at the damaged output port. (C) OSA spectrum of an edge comb versus average pump power. The white dashed line marks the OPO threshold. The color scale is in decibels (0 dB = 1 mW). (D) High-resolution spectra of individual comb teeth ( $\mathrm{\mu }$ ) versus pump wavelength. Edge and bulk bands are shaded in green and gray, respectively. Five snapshots and cold-cavity resonances are included. (E) Linewidths of nested longitudinal edge modes ( $\mathrm{\sigma }$ ), with cold-cavity linewidths shown for comparison. Inset: example fit of a nested tooth. FWHM, full width at half maximum. (F) Optical linewidth of the $\mathrm{\sigma }=2$ tooth versus pump wavelength. Red shading in (E) and (F) indicates estimated pump linewidth uncertainty, arising from jitter and OSA acquisition time (see fig. S6).

Fig. 3.. Two-timescale mode-locking and noise analysis.

(A) Quadratic variation of the comb teeth optical linewidth for an edge comb with a pump wavelength of 1547.86 nm (nested tooth $\mathrm{\sigma }=3$ ) across several longitudinal modes of the fast (750 GHz) and slow (2.5 GHz) timescales, indicated by $\mathrm{\mu }$ and $\mathrm{\sigma }$ , respectively. The data for the slow timescale shown in the inset are for (left) $\mathrm{\mu }=-1$ and (right) $\mathrm{\mu }=1$ . The blue curve and the red dashed line are the quadratic fit and the pump’s linewidth, respectively. (B) Optical linewidth variation over the fast timescale for a typical bulk comb (pump wavelength, 1547.91 nm), which lacks the quadratic form of the edge counterparts. The shaded red area in (A) and (B) indicates the estimated error for the pump linewidth (see fig. S6 for details). (C) Electrical spectrum analysis of the topological combs as a function of pump wavelength with an average pump power of $\approx$185 mW. The bulk and edge regions of the spectrum are highlighted in gray and green, respectively. (D) Peak position (blue) and Lorentzian linewidth analysis (red) of the repetition rates as a function of pump wavelength. The orange dashed line is the FT limit set by the 5-ns pulse duration of the pump (see section S11 for details). Note that, here, the uncertainties are smaller than the symbols. (E) Group delay measurement of the lattice in the linear regime using a weak tunable laser. (F) Repetition beats of an edge comb as a function of pump power. The white dashed line indicates the OPO threshold.

Fig. 4.. Temporal measurement of the device.

The output at the drop port is sent to a fast PD, with (A) an on-chip peak pump power of ~40 mW, which is well below the OPO threshold. Pumping the (B) edge and (C) bulk above the OPO threshold with 185-mW pump power. The plots include 2000 repeats of the experiment, with one example shown in blue and the average shown in red. (D to F) Corresponding FTs of the data in (A) to (C), respectively. (G) FT of the oscilloscope measurements of the topological combs as a function of discrete pump wavelength taken at every 30-pm intervals with an on-chip peak pump power of ~185 mW. The bulk and edge regions of the spectrum are marked. Each vertical strip includes 2000 repeats of the experiment. (H) Oscilloscope measurement of an edge comb as a function of pump power. The white dashed line indicates the OPO threshold.