Petri nets in epidemiology
- PMID: 40956342
- PMCID: PMC12441085
- DOI: 10.1007/s00285-025-02272-3
Petri nets in epidemiology
Abstract
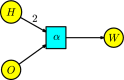
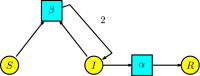
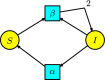
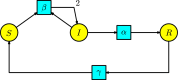
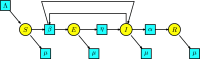
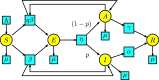
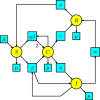
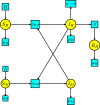
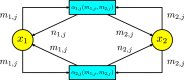
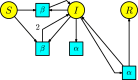
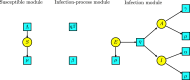
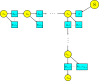
This work provides a geometric version of the next-generation matrix method for obtaining the basic reproduction number of an epidemiological model. We exhibit a certain correspondence between any system of ODEs and Petri nets. We observe that any epidemiological model has the basic structures found in the SIR model of Kermack-McKendrick. This means that the basic reproduction number depends only on three substructures inside the Petri net, which are also given by three Petri nets inside, representing the susceptible population, the infection process, and the infected population. The five assumptions of the next-generation matrix method given by van den Driessche-Watmough can be described geometrically using Petri nets. Thus, the next-generation matrix results in a matrix of flows between the infection compartments with a dominant eigenvalue given by the basic reproduction number.
Keywords: Basic reproduction number; Ordinary differential equations; Petri nets.
© 2025. The Author(s).
Conflict of interest statement
Declarations. Conflict of interest: The author declares no conflicts of interest.
Figures


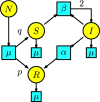
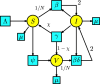
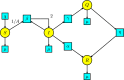
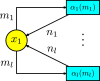

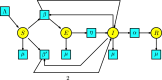
References
-
-
Diekmann O, Heesterbeek JAP, Metz JAJ (1990) On the definition and the computation of the basic reproduction ratio
 in models for infectious diseases in heterogeneous populations. J Math Biol 28(4):365–382
-
PubMed
in models for infectious diseases in heterogeneous populations. J Math Biol 28(4):365–382
-
PubMed
-
Diekmann O, Heesterbeek JAP, Metz JAJ (1990) On the definition and the computation of the basic reproduction ratio
-
- Driessche P, Watmough J (2002) Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci 180:29–48
-
- Driessche P, Watmough J (2008) Further notes on the basic reproduction number. In: Brauer, F., van den Driessche, P., Wu, J. (eds) Mathematical Epidemiology. Lecture Notes in Mathematics 1945, 159–178
-
- Reisig W (1982) Petri Nets: An Introduction. EATCS Monographs on Theoretical Computer Science, Springer-Verlag, ???
-
- Baez J, Biamonte JD (2018) Quantum Techniques in Stochastic Mechanics. World Scientific Publishing Co., ???
MeSH terms
LinkOut - more resources
Full Text Sources
Medical

